How to Calculate the Area of a Trapezoid

Finding the Area Using Height and Base Lengths

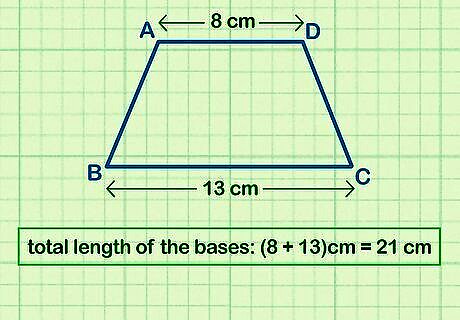
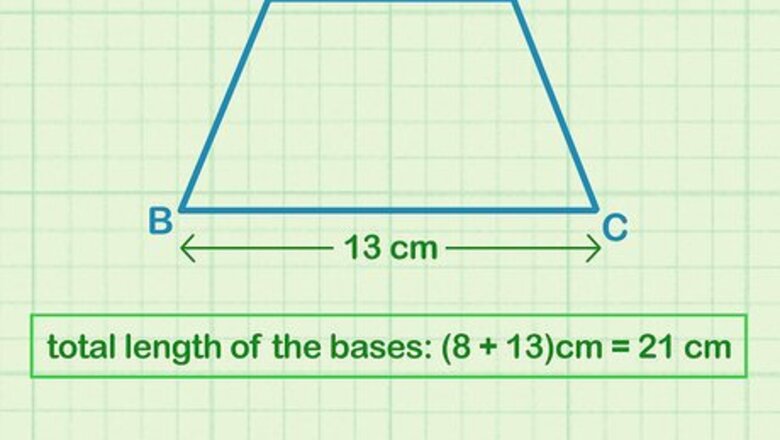
Add together the lengths of the bases. The bases are the 2 sides of the trapezoid that are parallel with one another. If you aren’t given the values for the base lengths, then use a ruler to measure each one. Add the 2 lengths together so you have 1 value. For example, if you find that the top base (b1) is 8 cm and the bottom base (b2) is 13 cm, the total length of the bases is 21 (8 cm + 13 cm = 21 cm, which reflects the "b = b1 + b2" part of the equation).

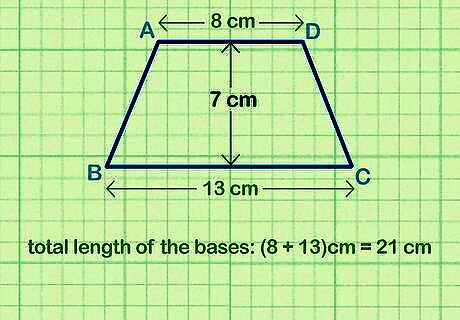
Measure the height of the trapezoid. The height of the trapezoid is the distance between the parallel bases. Draw a line between the bases, and use a ruler or other measuring device to find the distance. Write the height down so you don’t forget it later in your calculation. The length of the angled sides, or the legs of the trapezoid, is not the same as the height. The leg length is only the same as the height if the leg is perpendicular to the bases.

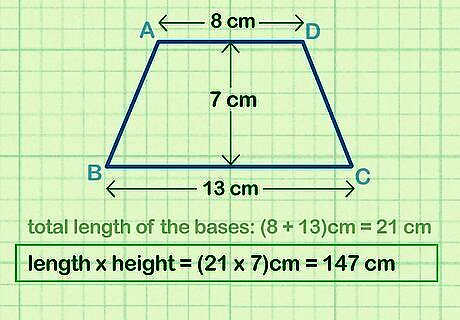
Multiply the total base length and height together. Take the sum of the base lengths you found (b) and the height (h) and multiply them together. Write the product in the appropriate square units for your problem. In this example, 21 cm x 7 cm = 147 cm which reflects the "(b)h" part of the equation.

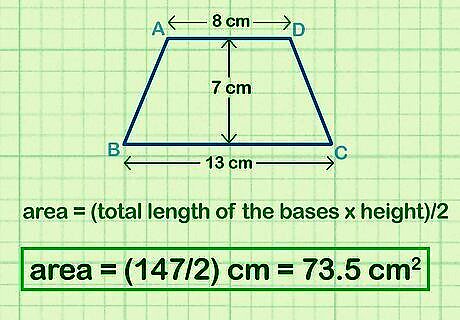
Multiply the product by ½ to find the area of the trapezoid. You can either multiply the product by ½ or divide the product by 2 to get the final area of the trapezoid since the result will be the same. Make sure you label your final answer in square units. For this example, 147 cm / 2 = 73.5 cm, which is the area (A).

Calculating Area of a Trapezoid If You Know the Sides

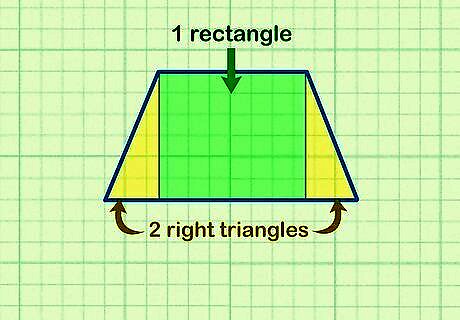
Break the trapezoid into 1 rectangle and 2 right triangles. Draw straight lines down from the corners of the top base so they intersect and form 90-degree angles with the bottom base. The inside of the trapezoid will have 1 rectangle in the middle and 2 triangles on either side that are the same size and have 90-degree angles. Drawing the shapes helps you visualize the area better and helps you find the height of the trapezoid. This method only works for regular trapezoids.

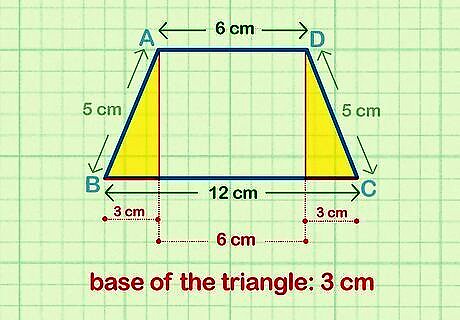
Find the length of one of the triangle’s bases. Subtract the length of the top base from the length of the bottom base to find the amount that’s left over. Divide the amount by 2 to find the length of the triangle’s base. You should now have the length of the base and the hypotenuse of the triangle. For example, if the top base (b1) is 6 cm and the bottom base (b2) is 12 cm, then the base of the triangle is 3 cm (because b = (b2 - b1)/2 and (12 cm - 6 cm)/2 = 6 cm which can be simplified to 6 cm/2 = 3 cm).

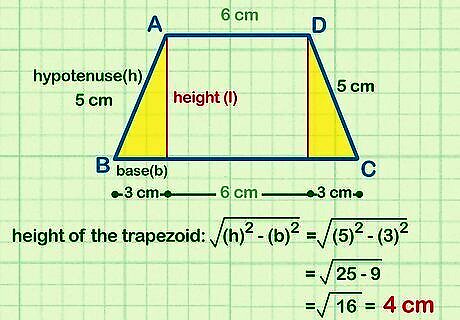
Use the Pythagorean theorem to find the height of the trapezoid. Plug the values for the length of the base and the hypotenuse, or the longest side of the triangle, into A + B = C, where A is the base and C is the hypotenuse. Solve the equation for B to find the height of the trapezoid. If the length of the base you found is 3 cm and the length of the hypotenuse is 5 cm, then in this example: Fill in the variables: (3 cm) + B = (5 cm) Simplify the squares: 9 cm +B = 25 cm Subtract 9 cm from each side: B = 16 cm Take the square root of each side: B = 4 cmTip: If you don’t have a perfect square in your equation, then simplify it as much as possible and leave a value with a square root. For example, √32 = √(16)(2) = 4√2.

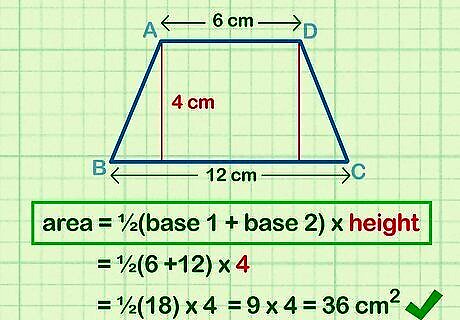
Plug the base lengths and height into the area formula and simplify it. Put the base lengths and the height into the formula A = ½(b1 +b2)h to find the area of the trapezoid. Simplify the number as much as you can and label it with square units. Write the formula: A = ½(b1+b2)h Fill in the variables: A = ½(6 cm +12 cm)(4 cm) Simplify the terms: A = ½(18 cm)(4 cm) Multiply the numbers together: A = 36 cm.