
views
In maths problems, one can encounter either of two options: constructing the tangent from a point outside of the circle, or constructing the tangent to a circle at a point on the circle.
Constructing a Tangent Line from a Point Outside of the Circle

Setup of the problem. Construct a line, tangent to the circle, passing through point P {\displaystyle P} P.
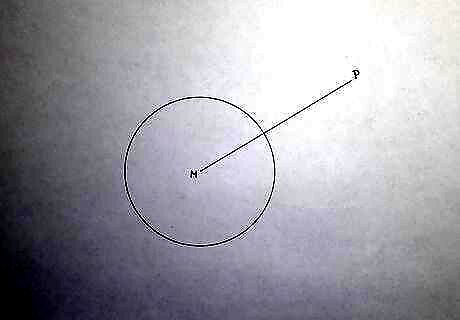
Connect the point P {\displaystyle P} P with the centre of the circle. You must first find the centre of the circle if it has not been given to you.
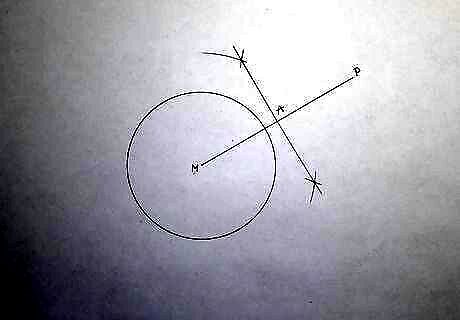
Bisect O P {\displaystyle OP} OP. The bisector intersects O P {\displaystyle OP} OP in A {\displaystyle A} A.
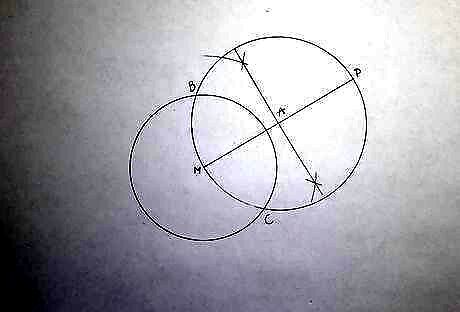
Construct a circle with radius A P {\displaystyle AP} AP, centred at A {\displaystyle A} A. This circle intersects the original circle at points B {\displaystyle B} B and C {\displaystyle C} C.
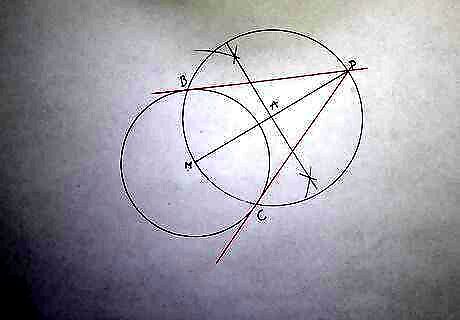
Connect P {\displaystyle P} P with B {\displaystyle B} B or C {\displaystyle C} C. Both P B {\displaystyle PB} PB an P C {\displaystyle PC} PC are tangent to the circle.
Erase any construction lines, if needed.
Constructing a Tangent Line to a Circle at a Point on the Circle

Setup of the problem. Construct a line, tangent to the circle at P {\displaystyle P} P.
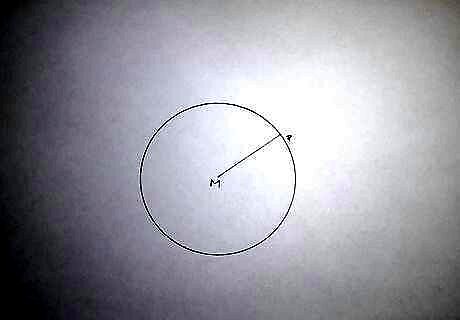
Draw the radius M P {\displaystyle MP} MP. You must first find the centre of the circle if it has not been given to you.
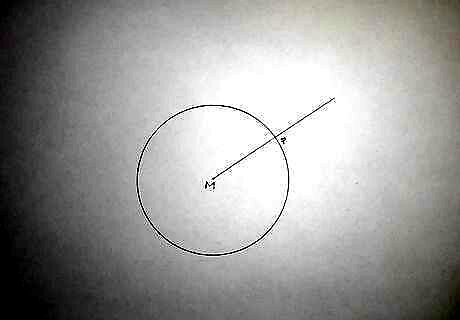
Extend the radius past the circle.

Construct the perpendicular to the radius through point P {\displaystyle P} P. That perpendicular is the tangent to the circle at point P {\displaystyle P} P.
Erase any construction lines, if needed.

















Comments
0 comment