
views
- To multiply scientific notation, first multiply the coefficients, then use the rule of exponents to multiply the bases.
- If the new coefficient is less than 10, multiply the new number by the new power of 10 to get your solution.
- If the new coefficient is more than 10, convert it to scientific notation and multiply it by the new power of 10.
Multiply the coefficients.
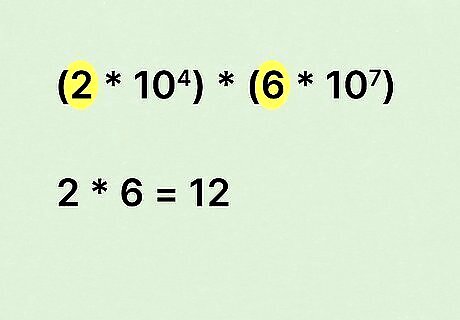
Start by multiplying the whole numbers in the equation. When you multiply scientific notation, you can break things up into whole numbers vs powers of 10. To get your new coefficient, simply multiply the whole numbers together. For example: Let’s say our problem is ( 2 × 10 4 ) × ( 6 × 10 7 ) {\displaystyle (2\times 10^{4})\times (6\times 10^{7})} {\displaystyle (2\times 10^{4})\times (6\times 10^{7})} Our first step would be to multiply the coefficients: 2 × 6 = 12 {\displaystyle 2\times 6=12} {\displaystyle 2\times 6=12}
Multiply the bases.

Use the rule of exponents to multiply the powers of 10. The rule of exponents tells us that when we multiply powers of 10, all we need to do is add the exponents together. This will give us our base. To continue our example from above, multiplying the bases would look like this: 10 4 × 10 7 {\displaystyle 10^{4}\times 10^{7}} {\displaystyle 10^{4}\times 10^{7}} Using the rule of exponents, we would convert the problem to 10 4 + 10 7 = 10 11 {\displaystyle 10^{4}+10^{7}=10^{11}} {\displaystyle 10^{4}+10^{7}=10^{11}}, because 4 + 7 = 11 {\displaystyle 4+7=11} {\displaystyle 4+7=11}
Multiply whole numbers by the new power of 10.
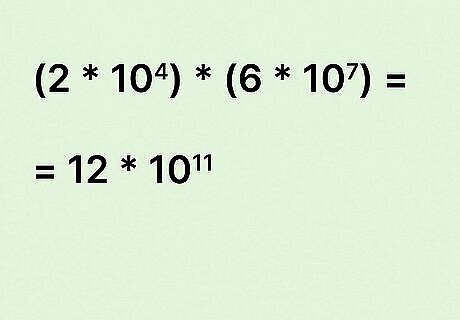
If your new coefficient is a whole number, combine it with your new base. If you finish up your problem and there are no decimals to deal with, then you’re done! Simply multiply your whole number by the new power of 10 to get the answer. In our example above, our answer would be 12 × 10 11 {\displaystyle 12\times 10^{11}} {\displaystyle 12\times 10^{11}}
Convert the number to scientific notation if needed.
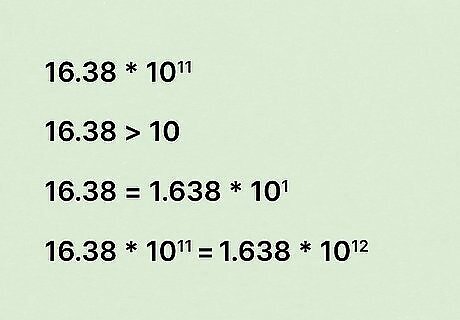
If your coefficient is not in scientific notation, convert it to scientific notation. To do that, move the decimal point to the left, then count how many times it’s moved. After that, multiply your new base by the base you solved for to get your answer. For example: ( 2.3 × 10 4 ) × ( 6.6 × 10 7 ) {\displaystyle (2.3\times 10^{4})\times (6.6\times 10^{7})} {\displaystyle (2.3\times 10^{4})\times (6.6\times 10^{7})} ( 2.3 × 6.6 = 16.38 ) × ( 10 4 × 10 7 ) {\displaystyle (2.3\times 6.6=16.38)\times (10^{4}\times 10^{7})} {\displaystyle (2.3\times 6.6=16.38)\times (10^{4}\times 10^{7})} 16.38 × 10 11 {\displaystyle 16.38\times 10^{11}} {\displaystyle 16.38\times 10^{11}} Since your coefficient is not in scientific notation (because it’s greater than 10), move the decimal point to the left and convert the problem to scientific notation: 1.638 × 10 1 {\displaystyle 1.638\times 10^{1}} {\displaystyle 1.638\times 10^{1}} Now, multiply that base by the base we solved for earlier: 10 1 × 10 11 {\displaystyle 10^{1}\times 10^{11}} {\displaystyle 10^{1}\times 10^{11}} The answer is 1.638 × 10 12 {\displaystyle 1.638\times 10^{12}} {\displaystyle 1.638\times 10^{12}}















Comments
0 comment