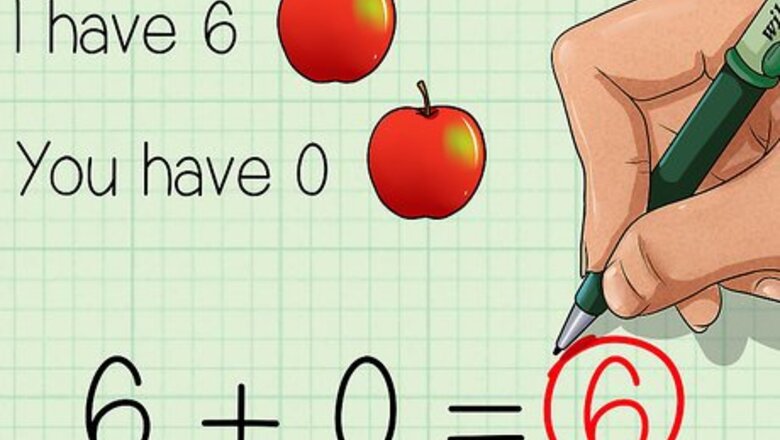
views
Adding with Mental Math
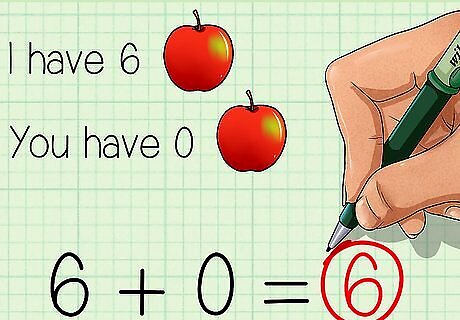
Understand the value of 0. Adding zero to a number does not change its value. For example, if I have 6 apples, and you have 0 apples, together we have 6 apples: 6 + 0 = 6 {\displaystyle 6+0=6} 6+0=6
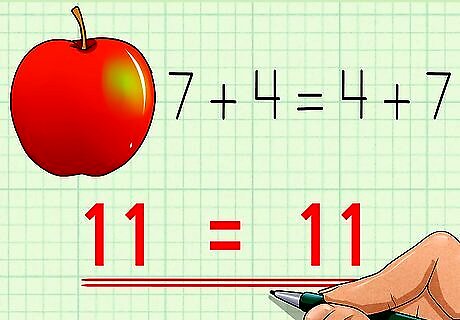
Understand the commutative property. The commutative property states that numbers can be added in any order. For example, 7 apples plus 4 apples is the same as 4 apples plus 7 apples. They both equal 11 apples: 7 + 4 = 4 + 7 {\displaystyle 7+4=4+7} 7+4=4+7 11 = 11 {\displaystyle 11=11} 11=11
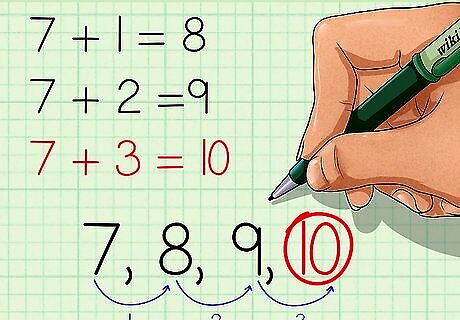
Add by counting on. Use the commutative property and start with the larger number, then count up the value of the smaller number. This strategy works best when one of the addends is less than five. Students can use their fingers or manipulatives to keep track of how many they count on. For example, to calculate 7 + 3 {\displaystyle 7+3} 7+3, begin with 7 and count on three: “Seven, eight, nine, ten.”
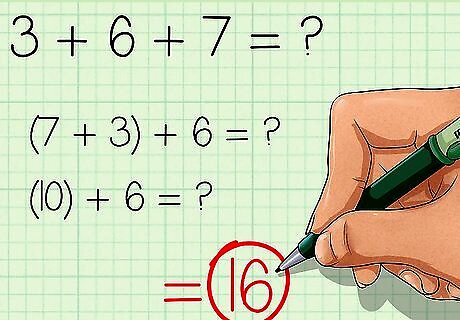
Make a ten when adding three or more numbers. Use the commutative property to make a ten, then add the remaining number. For example, to calculate 3 + 6 + 7 {\displaystyle 3+6+7} 3+6+7, first make a ten by adding 7 and 3, then add 6: 3 + 6 + 7 {\displaystyle 3+6+7} 3+6+7 ( 7 + 3 ) + 6 {\displaystyle (7+3)+6} (7+3)+6 ( 10 ) + 6 = 16 {\displaystyle (10)+6=16} (10)+6=16

Memorize doubles. A double is an addition sentence that adds a number to itself. Adding a number to itself yields a number twice as big as the original number, so if students know how to multiply by two, they can use multiplication to help them add. For example, students can memorize doubles up to 10: 1 + 1 = 2 {\displaystyle 1+1=2} 1+1=2 2 + 2 = 4 {\displaystyle 2+2=4} 2+2=4 3 + 3 = 6 {\displaystyle 3+3=6} 3+3=6 4 + 4 = 8 {\displaystyle 4+4=8} 4+4=8 5 + 5 = 10 {\displaystyle 5+5=10} 5+5=10 6 + 6 = 12 {\displaystyle 6+6=12} 6+6=12 7 + 7 = 14 {\displaystyle 7+7=14} 7+7=14 8 + 8 = 16 {\displaystyle 8+8=16} 8+8=16 9 + 9 = 18 {\displaystyle 9+9=18} 9+9=18 10 + 10 = 20 {\displaystyle 10+10=20} 10+10=20
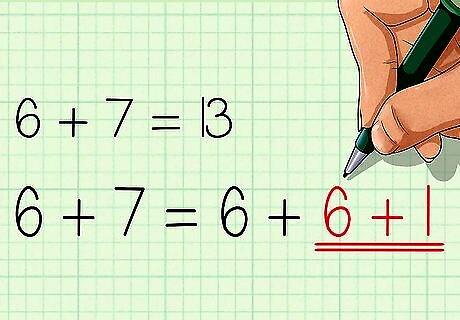
Recognize doubles plus one. A doubles plus one is an addition sentence that would be a double, except one number is one larger than the other. Once students have their doubles memorized, they can simply add 1 to the doubles sum. For example, if a student knows that 6 + 6 = 12 {\displaystyle 6+6=12} 6+6=12, they can recognize that 6 + 7 = 13 {\displaystyle 6+7=13} 6+7=13, because 6 + 7 = 6 + 6 + 1 {\displaystyle 6+7=6+6+1} 6+7=6+6+1.

Use skip counting. Students can use skip counting when adding by twos, fives, or tens. Students should recognize that any even number plus two will equal an even number, and any odd number plus two will equal an odd number. For example, 5 + 5 + 5 {\displaystyle 5+5+5} 5+5+5 is the same as skip counting by fives three times: “Five, ten, fifteen.”
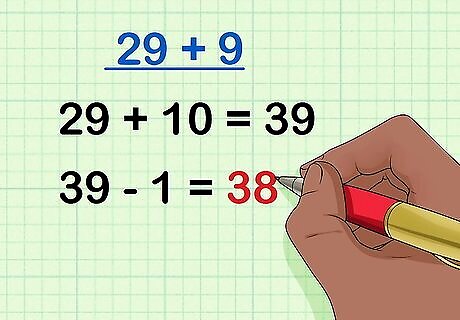
Think of plus 9 as plus 10 minus 1. To do this, whenever you add by 9, add by 10 instead, and then subtract 1 from the sum. For example, to calculate 29 + 9 {\displaystyle 29+9} 29+9, calculate: 29 + 10 = 39 {\displaystyle 29+10=39} 29+10=39 39 − 1 = 38 {\displaystyle 39-1=38} 39-1=38
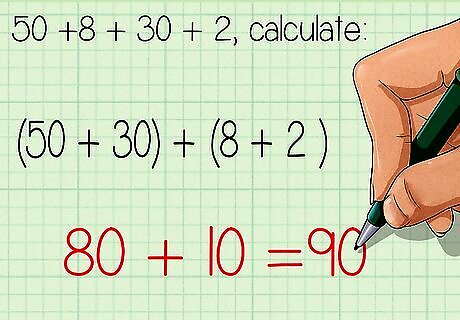
Break up larger numbers to make compatible numbers. Compatible numbers are numbers that are easier to add together. For example, to calculate 58 + 32 {\displaystyle 58+32} 58+32, you can break up 58 into 50 + 8 {\displaystyle 50+8} 50+8, and you can break up 32 into 30 + 2 {\displaystyle 30+2} 30+2. Then you can use the commutative property to add compatible numbers first: 50 + 8 + 30 + 2 {\displaystyle 50+8+30+2} 50+8+30+2 ( 50 + 30 ) + ( 8 + 2 ) {\displaystyle (50+30)+(8+2)} (50+30)+(8+2) 80 + 10 = 90 {\displaystyle 80+10=90} 80+10=90
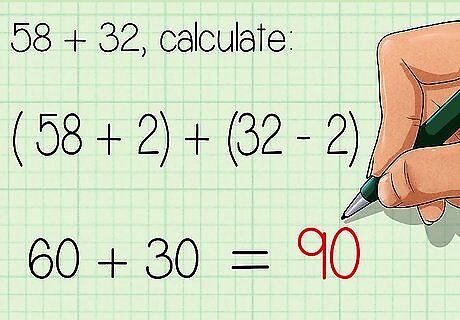
Balance numbers before adding. To balance numbers, you can subtract from one number and add the same amount to the other. For example, to find 58 + 32 {\displaystyle 58+32} 58+32, you could subtract 2 from 30, then add 2 to 58. 58 + 32 {\displaystyle 58+32} 58+32 ( 58 + 2 ) + ( 32 − 2 ) {\displaystyle (58+2)+(32-2)} (58+2)+(32-2) 60 + 30 = 90 {\displaystyle 60+30=90} 60+30=90
Subtracting with Mental Math
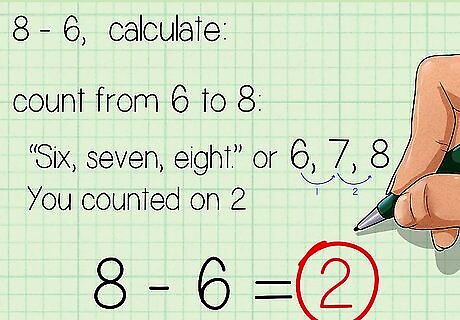
Count on from the number you are subtracting (the subtrahend) to the number you are subtracting from (the minuend). The result will be the answer, or difference. Students can use their fingers or manipulatives to count on. For example, to calculate 8 − 6 {\displaystyle 8-6} 8-6, start with 6 and see how many you have to count on to get to 8: “Six, seven, eight.” You counted on 2, so 8 − 6 = 2 {\displaystyle 8-6=2} 8-6=2.
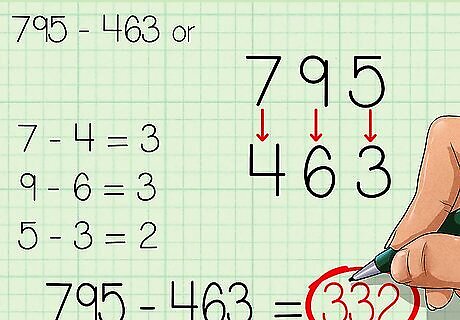
Use the front end strategy for problems that require no borrowing. To do this, subtract the digits beginning with the largest place value, ending with the lowest place value. When subtracting with pencil and paper you usually start from the ones place. When using the front end strategy, you work beginning from the other direction. This strategy only works when you do not have to borrow from other place values. You will know that the problem requires no borrowing if, when you line up the place values of each number, all the digits you are subtracting are smaller than the digits you are subtracting from. For example, to calculate 795 − 463 {\displaystyle 795-463} 795-463, you would first subtract the hundreds place, then the tens place, then the ones place: 7 − 4 = 3 {\displaystyle 7-4=3} 7-4=3 9 − 6 = 3 {\displaystyle 9-6=3} 9-6=3 5 − 3 = 2 {\displaystyle 5-3=2} 5-3=2So 795 − 463 = 332 {\displaystyle 795-463=332} 795-463=332.

Break up the subtrahend into tens and ones. Then subtract your group of tens, then subtract the group of ones. You can also use this strategy to break up numbers into hundreds and tens, or larger place values, for easier subtraction. For example, to calculate 42 − 24 {\displaystyle 42-24} 42-24, break up 24 into 20 and 4: 42 − 24 {\displaystyle 42-24} 42-24 ( 42 − 20 ) − 4 {\displaystyle (42-20)-4} (42-20)-4 ( 22 ) − 4 = 18 {\displaystyle (22)-4=18} (22)-4=18
Multiplying with Mental Math
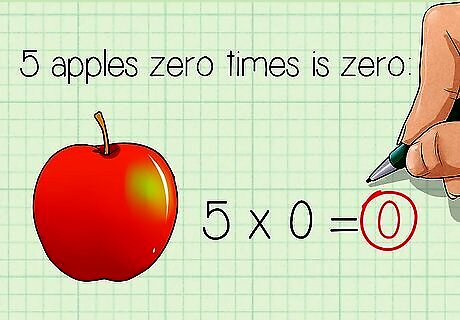
Understand the value of 0. A number multiplied by 0 will always equal 0. For example, 5 apples zero times is zero: 5 × 0 = 0 {\displaystyle 5\times 0=0} 5\times 0=0.
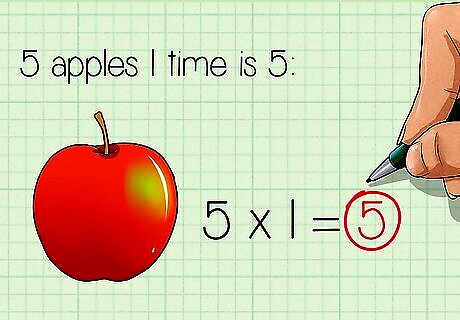
Understand the value of 1. A number multiplied by 1 will always equal the number. For example, 5 apples 1 time is 5: 5 × 1 = 5 {\displaystyle 5\times 1=5} 5\times 1=5.
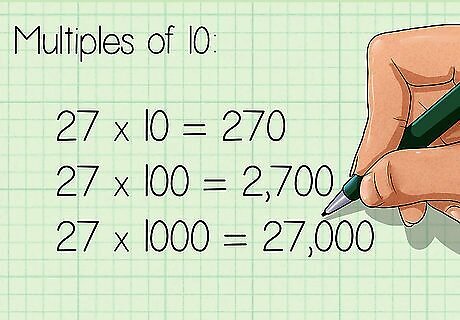
Use the shortcut for multiples of ten. The shortcut is that, when multiplying any number by a multiple of ten, simply add the number of zeroes in the multiple to the other number. For example: 27 × 10 = 270 {\displaystyle 27\times 10=270} 27\times 10=270 27 × 100 = 2 , 700 {\displaystyle 27\times 100=2,700} 27\times 100=2,700 27 × 1000 = 27 , 000 {\displaystyle 27\times 1000=27,000} 27\times 1000=27,000
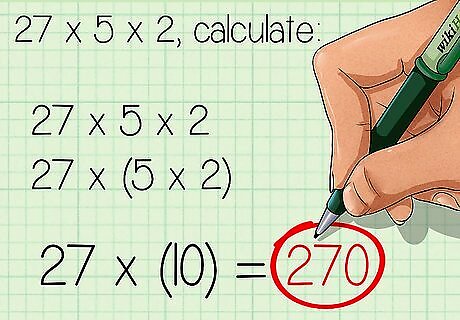
Use the associative property. The associative property states that you can change the order of groupings you multiply first. For example, to calculate 27 × 5 × 2 {\displaystyle 27\times 5\times 2} 27\times 5\times 2, multiplying the 5 and 2 first will make a ten, which makes the problem easier: 27 × 5 × 2 {\displaystyle 27\times 5\times 2} 27\times 5\times 2 27 × ( 5 × 2 ) {\displaystyle 27\times (5\times 2)} 27\times (5\times 2) 27 × ( 10 ) = 270 {\displaystyle 27\times (10)=270} 27\times (10)=270
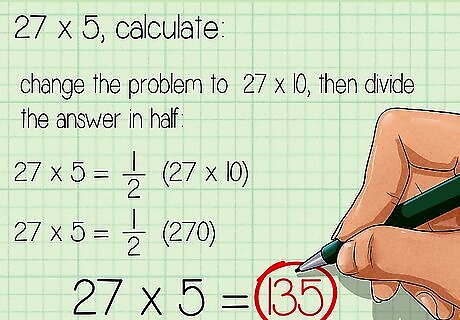
Use the factor of 5 as half the factor of 10. To do this, whenever you are multiplying a number by 5, multiply by 10 instead, and then half the product. For example, to calculate 27 × 5 {\displaystyle 27\times 5} 27\times 5, change the problem to 27 × 10 {\displaystyle 27\times 10} 27\times 10, then divide the answer in half: 27 × 5 = 1 2 ( 27 × 10 ) {\displaystyle 27\times 5={\frac {1}{2}}(27\times 10)} 27\times 5={\frac {1}{2}}(27\times 10) 27 × 5 = 1 2 ( 270 ) {\displaystyle 27\times 5={\frac {1}{2}}(270)} 27\times 5={\frac {1}{2}}(270) 27 × 5 = 135 {\displaystyle 27\times 5=135} 27\times 5=135

Break up numbers into compatible factors. Compatible numbers are numbers that are easier to multiply. For example, to calculate 125 × 8 {\displaystyle 125\times 8} 125\times 8, you can factor 125 as 25 × 5 {\displaystyle 25\times 5} 25\times 5 and 8 as 4 × 2 {\displaystyle 4\times 2} 4\times 2. You can then use the commutative and associative property to multiply the factors in any order or combination. Thus: 125 × 8 {\displaystyle 125\times 8} 125\times 8 ( 25 × 5 ) × ( 4 × 2 ) {\displaystyle (25\times 5)\times (4\times 2)} (25\times 5)\times (4\times 2) ( 25 × 4 ) × ( 5 × 2 ) {\displaystyle (25\times 4)\times (5\times 2)} (25\times 4)\times (5\times 2) 100 × 10 = 1000 {\displaystyle 100\times 10=1000} 100\times 10=1000
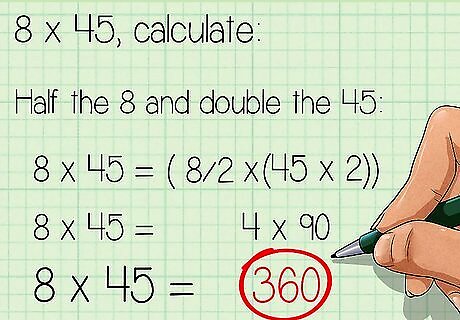
Double one number and half the other. This is another way of finding compatible numbers that are easier to multiply. For example, to calculate 8 × 45 {\displaystyle 8\times 45} 8\times 45, you could half the 8 and double the 45: 8 × 45 = 4 × 90 {\displaystyle 8\times 45=4\times 90} 8\times 45=4\times 90 8 × 45 = 360 {\displaystyle 8\times 45=360} 8\times 45=360
Dividing with Mental Math

Use the distributive property. To do this, break up the number you are dividing into smaller numbers that can easily be divided by the divisor. Then, sum the quotients. For example, to calculate 104 ÷ 8 {\displaystyle 104\div 8} 104\div 8, break up the 104 into 64 and 40: 104 ÷ 8 {\displaystyle 104\div 8} 104\div 8 ( 64 + 40 ) ÷ 8 {\displaystyle (64+40)\div 8} (64+40)\div 8 ( 64 ÷ 8 ) + ( 40 ÷ 8 ) {\displaystyle (64\div 8)+(40\div 8)} (64\div 8)+(40\div 8) ( 8 ) + ( 5 ) = 13 {\displaystyle (8)+(5)=13} (8)+(5)=13

Use the shortcut for multiples of ten. The shortcut is that, when dividing any number by a multiple of ten, simply subtract the number of zeroes in the multiple from the other number. For example: 27 , 000 ÷ 10 = 2 , 700 {\displaystyle 27,000\div 10=2,700} 27,000\div 10=2,700 27 , 000 ÷ 100 = 270 {\displaystyle 27,000\div 100=270} 27,000\div 100=270 27 , 000 ÷ 1 , 000 = 27 {\displaystyle 27,000\div 1,000=27} 27,000\div 1,000=27
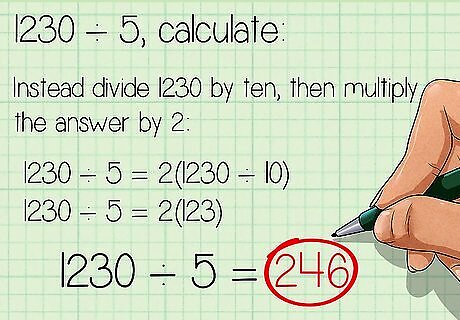
Use the divisor 5 as half the divisor of 10. Whenever you are dividing a number by five, you can instead divide the number by ten, then multiply the quotient by 2. For example, to calculate 1230 ÷ 5 {\displaystyle 1230\div 5} 1230\div 5, instead divide 1230 by ten, then multiply the answer by 2: 1230 ÷ 5 = 2 ( 1230 ÷ 10 ) {\displaystyle 1230\div 5=2(1230\div 10)} 1230\div 5=2(1230\div 10) 1230 ÷ 5 = 2 ( 123 ) {\displaystyle 1230\div 5=2(123)} 1230\div 5=2(123) 1230 ÷ 5 = 246 {\displaystyle 1230\div 5=246} 1230\div 5=246

















Comments
0 comment