
views
- Read problem instructions carefully. Look for key words like “solve,” “simplify,” “factor,” or “reduce" so you know what action to perform.
- Use the order of operations to solve problems in the proper sequence: Parentheses, Exponents, Multiplication, Division, Addition, Subtraction.
- Remember that an equation has an equal sign and can be solved. An expression can only be factored or simplified.
Algebra Objectives
Read the problem instructions carefully. When you have one or more algebra problems, you must read the instructions carefully. Look for key words in the instructions like “solve,” “simplify,” “factor,” or “reduce.” These are some of the most common instructions (although there are others that you will learn). Many people have problems because they try to “solve” a problem when they really only need to “simplify” it.
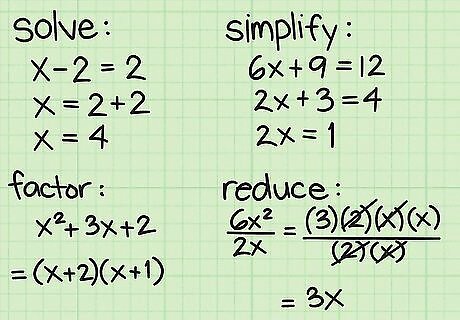
Perform the operations that are instructed. When you read the problem instructions, you should identify the key words and then perform those operations. Many people feel frustration with algebra when they try doing something that is not really part of the intended problem. The basic operations you will be asked for are: Solve. You will need to reduce the problem to an actual numerical solution, such as “x=4.” You need to find a value for the variable that can make the problem come true. Simplify. You need to manipulate the problem into some simpler form than before, but you will not wind up with what you might consider “an answer.” You will probably not have a single numerical value for the variable. Factor. This is similar to “simplify,” and is usually used with complex polynomials or fractions. You need to find a way to turn the problem into smaller terms. Just as the number 12 can be broken into factors of 3x4, for example, you can factor an algebraic polynomial. For example, a simple expression like 5 x {\displaystyle 5x} 5x can be broken into factors of 5 {\displaystyle 5} 5 and x {\displaystyle x} x. For example, the expression x 2 + 3 x + 2 {\displaystyle x^{2}+3x+2} x^{2}+3x+2 can be factored into the terms ( x + 2 ) {\displaystyle (x+2)} (x+2) and ( x + 1 ) {\displaystyle (x+1)} (x+1). Reduce. To “reduce” a problem generally involves a combination of factoring and then simplifying. You would break the terms of a numerator and denominator into their factors. Then look for common factors on top and bottom, and cancel them out. Whatever remains is the “reduced” form of the original problem. For example, reduce the expression 6 x 2 2 x {\displaystyle {\frac {6x^{2}}{2x}}} {\frac {6x^{2}}{2x}} as follows: 1. Factor the numerator and denominator: ( 3 ) ( 2 ) ( x ) ( x ) ( 2 ) ( x ) {\displaystyle {\frac {(3)(2)(x)(x)}{(2)(x)}}} {\frac {(3)(2)(x)(x)}{(2)(x)}} 2. Look for common terms. Both the numerator and denominator have factors of 2 and x. 3. Eliminate the common terms: ( 3 ) ( 2 ) ( x ) ( x ) ( 2 ) ( x ) {\displaystyle {\frac {(3)(2)(x)(x)}{(2)(x)}}} {\frac {(3)(2)(x)(x)}{(2)(x)}} 4. Copy down what remains: 3 x {\displaystyle 3x} 3x
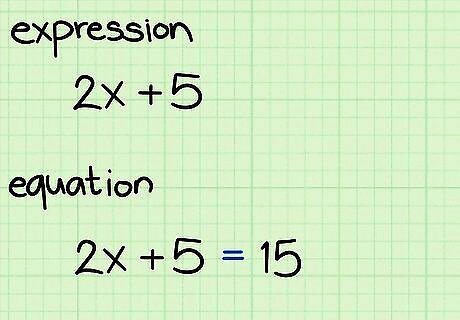
Learn the difference between “expression” and “equation.” In algebra, the difference between an “expression” and an “equation” is very important. An expression is any group of numbers and variables, collected together. Some examples of expressions are x {\displaystyle x} x, 14 x y z {\displaystyle 14xyz} 14xyz and 2 x + 15 {\displaystyle {\sqrt {2x+15}}} {\sqrt {2x+15}}. All you can do to an expression is simplify or factor it. An equation, on the other hand, contains an = sign. You can simplify or factor equations, but you can also solve them to get a final answer. It is important to look for the difference. If you have an expression, like 4 x 2 {\displaystyle 4x^{2}} 4x^{2}, you can never find a single “answer” or “solution.” You could find out that if x = 1 {\displaystyle x=1} x=1, then the expression would have a value of 4, and if x = 2 {\displaystyle x=2} x=2, then the expression would have a value of ( 4 ) ( 2 ) 2 {\displaystyle (4)(2)^{2}} (4)(2)^{2}, which is 16. But you cannot get a single “answer."
Order of Operations

Learn PEMDAS. In algebra, the steps you take must occur in a logical order, which is called the “order of operations.” This is often simplified by the mnemonic device “PEMDAS.” The letters of PEMDAS will help you know which operations to perform in order. The letters of PEMDAS stand for: Parentheses. Exponents. Multiplication. Division. Addition. Subtraction.

Perform operations inside parentheses first. When you have an expression or equation that includes terms inside parentheses, you need to do whatever is inside the parentheses first. Consider the difference between 5 ∗ 3 + 2 {\displaystyle 5*3+2} 5*3+2 and 5 ∗ ( 3 + 2 ) {\displaystyle 5*(3+2)} 5*(3+2). Without the parentheses, the first expression , 5 ∗ 3 + 2 {\displaystyle 5*3+2} 5*3+2, would become 15 + 2 = 17 {\displaystyle 15+2=17} 15+2=17. With the parentheses, 5 ∗ ( 3 + 2 ) {\displaystyle 5*(3+2)} 5*(3+2), you perform the (3+2) first, so the simplified expression becomes 5 ∗ 5 = 25 {\displaystyle 5*5=25} 5*5=25.

Simplify any exponents next. Exponents need to be performed as the next part of simplifying or solving a problem. Consider the expression 3 ∗ 2 2 {\displaystyle 3*2^{2}} 3*2^{2}. Without the order of operations, you wouldn’t know if you should first multiply 3 ∗ 2 {\displaystyle 3*2} 3*2 and then square the result, so your value is 36, or if you square the 2 first, then multiply by 3. Using PEMDAS, the correct operation is: 3 ∗ 2 2 {\displaystyle 3*2^{2}} 3*2^{2} 3 ∗ 4 {\displaystyle 3*4} 3*4…..Square the 2 first. 12 {\displaystyle 12} 12…..This is the expected result.
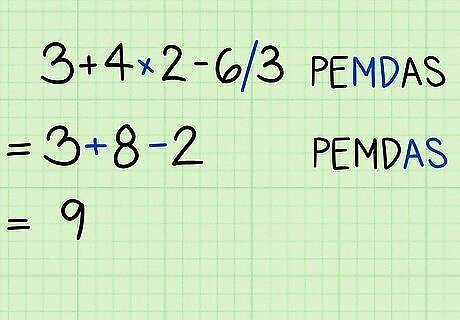
Multiply or divide, from right to left. M and D are the next two parts of PEMDAS, and they go together. After performing any exponents, you then perform multiplication or division from left to right. 3 + 4 ∗ 2 − 6 / 3 {\displaystyle 3+4*2-6/3} 3+4*2-6/3 3 + 8 − 2 {\displaystyle 3+8-2} 3+8-2…..4*2=8, and 6/3=2. These can be done in the same step.
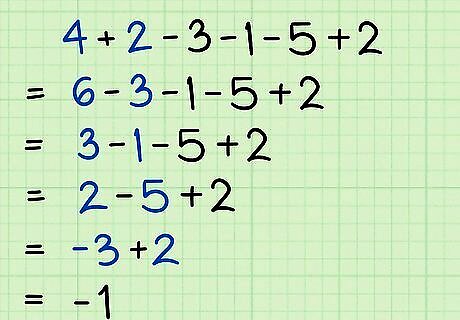
Add or subtract, from right to left. A and S are the final steps of PEMDAS. These mean that you add or subtract whatever terms remain in the expression. You can perform addition and subtraction in the same step, moving from right to left through the problem. Consider the expression 4 + 2 − 3 − 1 − 5 + 2 {\displaystyle 4+2-3-1-5+2} 4+2-3-1-5+2: 4 + 2 − 3 − 1 − 5 + 2 {\displaystyle 4+2-3-1-5+2} 4+2-3-1-5+2 6 − 3 − 1 − 5 + 2 {\displaystyle 6-3-1-5+2} 6-3-1-5+2…..(Add 4+2) 3 − 1 − 5 + 2 {\displaystyle 3-1-5+2} 3-1-5+2…..(Subtract 6-3) 2 − 5 + 2 {\displaystyle 2-5+2} 2-5+2…..(Subtract 3-1) − 3 + 2 {\displaystyle -3+2} -3+2…..(Subtract 2-5) − 1 {\displaystyle -1} -1…..(Add -3+1) If you perform the steps in any other order, you may come up with a different, incorrect result. For example, suppose you chose to do all the additions first, and then the subtractions: 4 + 2 − 3 − 1 − 5 + 2 {\displaystyle 4+2-3-1-5+2} 4+2-3-1-5+2 6 − 3 − 1 − 7 {\displaystyle 6-3-1-7} 6-3-1-7…..(Add 4+2 and add 5+2) 3 − 1 − 7 {\displaystyle 3-1-7} 3-1-7…..(Subtract 6-3) 2 − 7 {\displaystyle 2-7} 2-7…..(Subtract 3-1) − 5 {\displaystyle -5} -5…..(Subtract 2-7. This gives a result of -5, which is incorrect.)
Variables
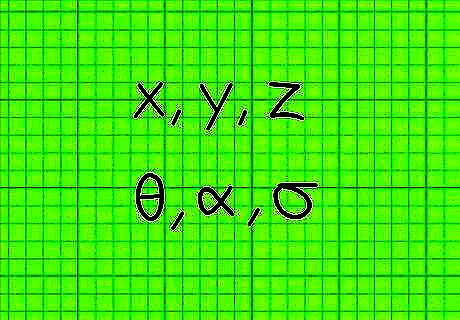
Get used to symbols other than numbers. In early math, you worked only with numbers. Learning algebra is about being able to solve problems with unknown terms. These unknown terms are represented in the problems with letters. You need to get used to treating these letters like numbers, although you may not know their actual value yet. Some common examples of variables include: Letters, such as x {\displaystyle x} x, y {\displaystyle y} y or z {\displaystyle z} z Greek symbols, such as θ {\displaystyle \theta } \theta , α {\displaystyle \alpha } \alpha or σ {\displaystyle \sigma } \sigma . Be aware that some symbols might look like variables but are actually known numbers. For example, the Greek symbol pi, π {\displaystyle \pi } \pi , stands for the number 3.1415.
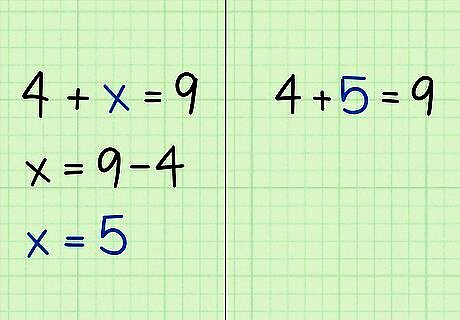
Consider the variable as an unknown place holder. If you think of the phrase, “Two times some number,” you can express that with a variable as 2 ∗ x {\displaystyle 2*x} 2*x. The variable x {\displaystyle x} x takes the place of the unknown “some number.” Usually, your job in an algebra problem is to find the value of the variable. For example, when you start with the equation 4 + x = 9 {\displaystyle 4+x=9} 4+x=9, you need to think, “What number added to 4 will make 9?” The solution is 5, which you can write algebraically as x = 5 {\displaystyle x=5} x=5.
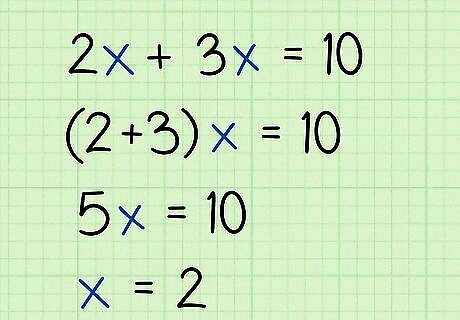
Combine common variables together. When you learn to treat the variables as numbers, you can combine or simplify them as you do with numbers. This is usually referred to as “combining like terms.” For example, 2 x + 3 x = 10 {\displaystyle 2x+3x=10} 2x+3x=10 just means that 2 of some variable added to 3 of the same variable will equal 10. If you have 2 of something and 3 of the same thing, you can add them together. Then, 2 x + 3 x {\displaystyle 2x+3x} 2x+3x will become 5x, so your problem is 5 x = 10 {\displaystyle 5x=10} 5x=10, and the solution is x = 2 {\displaystyle x=2} x=2. You can only add or subtract the same variable. Some algebra problems may contain two or more variables. In the problem 2 x + 3 y = 10 {\displaystyle 2x+3y=10} 2x+3y=10, you cannot combine the x {\displaystyle x} x and y {\displaystyle y} y terms together because the different variables represent different unknown numbers.
Inverse Operations
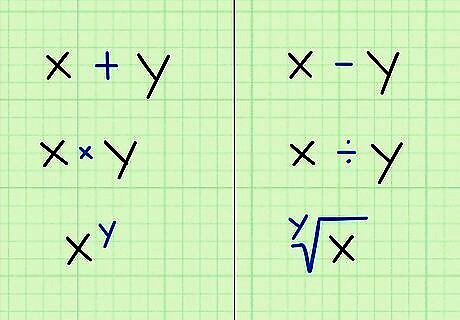
Learn the concept of inverse functions. One key to being successful in algebra is performing inverse functions. The word “inverse” means opposite. Inverse functions are a way of undoing or untangling a problem. If a chosen problem, for example, contains multiplication, you will use division, which is the inverse of multiplication, to solve the problem. The inverse of addition is subtraction. The inverse of subtraction is addition. The inverse of multiplication is division. The inverse of division is multiplication. The inverse of an exponent is a root (square root, cube root, etc.).
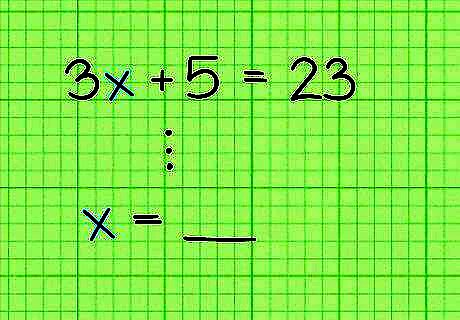
Focus on isolating the variable. If you are asked to “solve” an equation, this means that you want to end up with x = {\displaystyle x=} x=__, with some number in the blank space. You need to use algebra to move everything else away from the x {\displaystyle x} x term so it is alone on one side of the equals sign. You will do this with a series of inverse operations. The key rule to remember is that any operation you make to one side of the equation, you must also do the same to the opposite side of the equation. This will keep the equation balanced and still equal. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher To solve an equation for a variable like "x," you need to manipulate the equation to isolate x. Use techniques like the distributive property, combining like terms, factoring, adding or subtracting the same number, and multiplying or dividing by the same non-zero number to isolate "x" and find the answer.
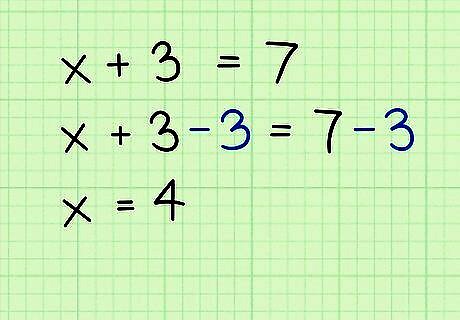
Cancel addition by using subtraction (and vice versa). Individual terms in an equation are linked by a combination of plus and minus signs. You can “cancel” these to get the variable alone by doing the opposite function. For example, if you start with x + 3 = 7 {\displaystyle x+3=7} x+3=7, you want the x {\displaystyle x} x alone. The inverse of + 3 {\displaystyle +3} +3 is − 3 {\displaystyle -3} -3. Remember that you must do everything equally to both sides of the equation. So you will get: x + 3 = 7 {\displaystyle x+3=7} x+3=7 x + 3 − 3 = 7 − 3 {\displaystyle x+3-3=7-3} x+3-3=7-3…..(subtract 3 equally on both sides) x = 4 {\displaystyle x=4} x=4…..(the +3 and -3 cancel each other out to leave the solution) If you start with a subtraction problem, you will cancel it the same way with addition: x − 8 = 12 {\displaystyle x-8=12} x-8=12 x − 8 + 8 = 12 + 8 {\displaystyle x-8+8=12+8} x-8+8=12+8…..(add 8 to both sides) x = 20 {\displaystyle x=20} x=20…..(the +8 and -8 cancel each other out to leave the solution)
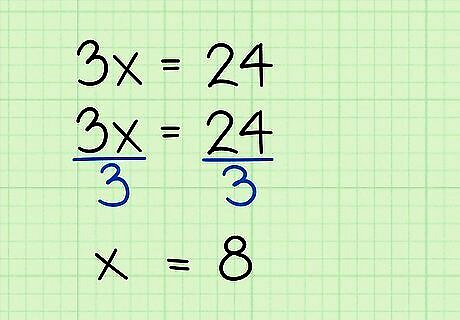
Cancel multiplication by using division (and vice versa). In the same way, you can perform inverse operations on multiplication and division. A term like 3 x {\displaystyle 3x} 3x means 3 ∗ x {\displaystyle 3*x} 3*x. To get the variable alone, you will divide. Remember that for an equation, you must divide both sides of the equation equally. Consider the problem 3 x = 24 {\displaystyle 3x=24} 3x=24. Since this is a multiplication problem, you will solve it with division: 3 x = 24 {\displaystyle 3x=24} 3x=24 3 x 3 = 24 3 {\displaystyle {\frac {3x}{3}}={\frac {24}{3}}} {\frac {3x}{3}}={\frac {24}{3}}…..(Divide both sides equally by 3. Note that the ÷ {\displaystyle \div } \div symbol is not usually used in algebra. Instead, show division by writing the terms as a fraction.) x = 8 {\displaystyle x=8} x=8…..(the 3s on the left cancel each other out to leave the solution) Do the same to cancel a division problem with multiplication. Consider the problem x 4 = 9 {\displaystyle {\frac {x}{4}}=9} {\frac {x}{4}}=9: x 4 = 9 {\displaystyle {\frac {x}{4}}=9} {\frac {x}{4}}=9 x 4 ∗ 4 = 9 ∗ 4 {\displaystyle {\frac {x}{4}}*4=9*4} {\frac {x}{4}}*4=9*4…..(multiply both sides by 4) x = 36 {\displaystyle x=36} x=36…..(the 4s on the left cancel each other out to leave the solution)
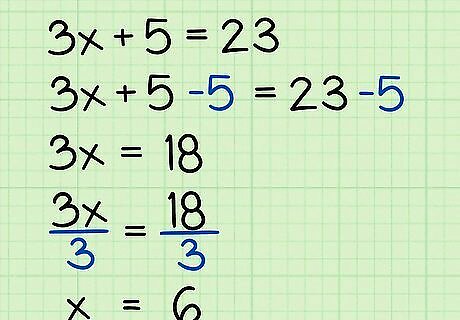
Use a combination of add/subtract and multiply/divide. As problems become more complicated, you may have to perform multiple operations to get to a solution. You will usually use addition and subtraction first, to isolate the variable with its coefficient. Then you will use multiplication or division to find the solution. 3 x + 5 = 23 {\displaystyle 3x+5=23} 3x+5=23 3 x + 5 − 5 = 23 − 5 {\displaystyle 3x+5-5=23-5} 3x+5-5=23-5…..(first, subtract 5 from both sides to leave the x term alone) 3 x = 18 {\displaystyle 3x=18} 3x=18…..(the +5 and -5 cancel out on the left) 3 x 3 = 18 3 {\displaystyle {\frac {3x}{3}}={\frac {18}{3}}} {\frac {3x}{3}}={\frac {18}{3}}…..(divide both sides by 3) x = 6 {\displaystyle x=6} x=6…..(the 3s on the left cancel each other out, leaving the solution)
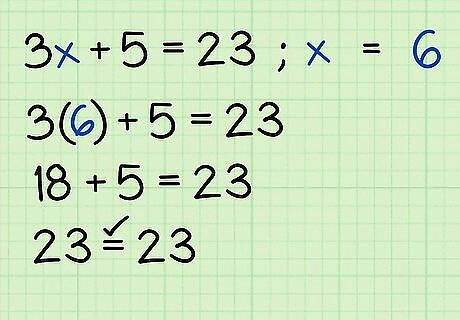
Check your result. In algebra, you can almost always find out if you have done the problem correctly by checking your answer. Take the solution that you found, and insert it back in the original problem in place of the variable. Then simplify the problem, and if you reach a true statement, you solution was correct. Try the example you just solved, 3 x + 5 = 23 {\displaystyle 3x+5=23} 3x+5=23. Put the solution of x = 6 {\displaystyle x=6} x=6 in place of the variable: 3 x + 5 = 23 {\displaystyle 3x+5=23} 3x+5=23 3 ( 6 ) + 5 = 23 {\displaystyle 3(6)+5=23} 3(6)+5=23…..(Insert the value x = 6 {\displaystyle x=6} x=6.) 18 + 5 = 23 {\displaystyle 18+5=23} 18+5=23…..(Simplify the equation.) 23 = 23 {\displaystyle 23=23} 23=23….. (This is true, so your solution of x = 6 {\displaystyle x=6} x=6 is correct.)
Foundational Math
Learn the basic math facts. Algebra is a system of manipulating numbers and operations to try to solve problems. When you learn algebra, you will learn the rules to follow for solving problems. But to help make that easier, you need to have a strong understanding of basic math facts. You should know basic addition, subtraction, multiplication and division facts and be able to work with them easily. In particular, you should be able to do the following: Add and subtract single digit numbers in your head quickly. Being able to work with two-digit numbers is even more helpful. Know your multiplication tables from 1 through 12. Know division and factors for numbers up through 144 (12x12).
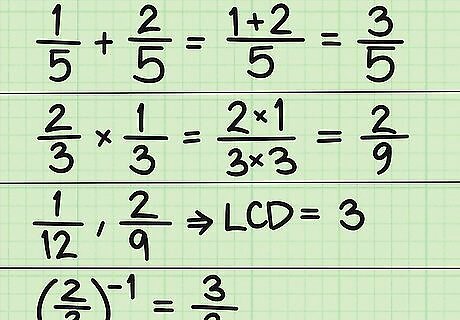
Practice the rules of fractions. Algebra uses the rules of fractions as much as any other numbering system. You need to be comfortable with finding common denominators, adding and subtracting fractions, multiplying and dividing fractions. When you learn algebra, you will expand this knowledge into working with unknown variables, but you need a strong understanding of the basics first. Know the importance of reciprocals. You need to know the concept of reciprocal numbers. The short definition of a reciprocal is that it is a fraction turned upside down. Thus, the reciprocal of 2 3 {\displaystyle {\frac {2}{3}}} {\frac {2}{3}} is 3 2 {\displaystyle {\frac {3}{2}}} {\frac {3}{2}}, and the reciprocal of 4 5 {\displaystyle {\frac {4}{5}}} {\frac {4}{5}} is 5 4 {\displaystyle {\frac {5}{4}}} {\frac {5}{4}}. You use reciprocals as an alternative to division, when the problem is complicated. Instead of dividing by one fraction, you can multiply by its reciprocal.
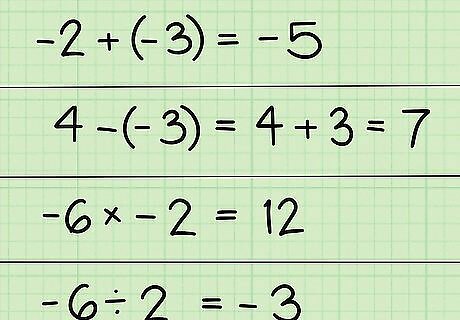
Know how to use negative numbers. You will often be using negative numbers or variables. You should review how to add, subtract, multiply, and divide negatives before starting to learn algebra. Here are some basic rules for working with negatives. You can also see our articles on adding and subtracting negative numbers and dividing and multiplying negative numbers. On a number line, a negative number is the same distance from zero as the positive, but in the opposite direction. A negative plus a negative will also be negative. Adding two negative numbers together makes the number more negative. Two negative signs together cancel each other out. Subtracting a negative number is the same as adding a positive number. 4-(-3) is the same as 4+3 = 7. Multiplying or dividing two negative numbers gives a positive answer. Multiplying or dividing one positive number and one negative number gives a negative answer.

















Comments
0 comment