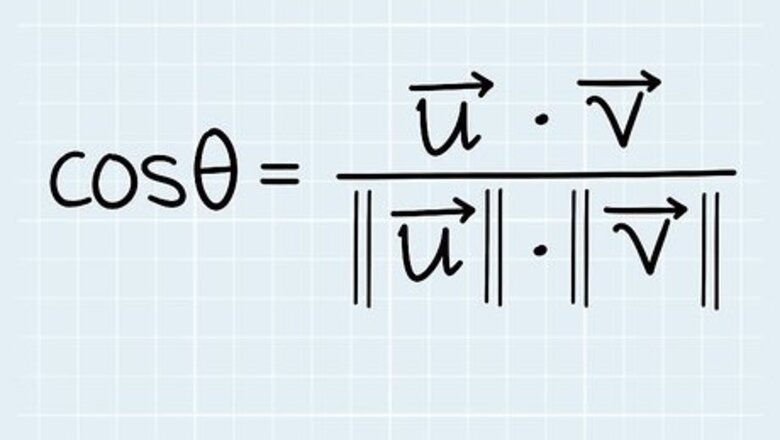
views
- Use the formula ( • ) / (|||| ||||) to find the angle between vectors using the dot product.
- To calculate the dot product, multiply the same direction coordinates of each vector and add the results together.
- Then, find each vector’s magnitude using the Pythagorean Theorem, or √(u12 + u22). Plug the arccos, dot product, and magnitudes into a calculator to get the angle.
- Or, use the cross product formula ( ) / (|||| ||||) to get the angle between the vectors.
Using the Dot Product Formula
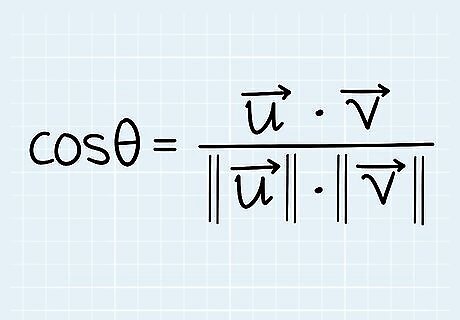
Use the formula: θ = c o s − 1 {\displaystyle \theta =cos^{-1}} {\displaystyle \theta =cos^{-1}} ( u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} • v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}) / (|| u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}}|| || v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}||). The angle between 2 vectors is where the tails of 2 vectors, or line segments, meet. Each vector has a magnitude, or length, and a direction that it’s heading. So, to find the angle between 2 vectors, you use the above formula where: θ {\displaystyle \theta } \theta is the angle between the vectors. c o s − 1 {\displaystyle cos^{-1}} cos^{{-1}} is the inverse of cosine, or the arc cos. u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} • v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}} is the dot product of vector u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} and v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}. || u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}}|| || v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}|| is the magnitude of vector u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} and v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}.

Identify the vectors’ coordinates in your math problem. Most math problems give you the dimensional coordinates of each vector, which are sometimes also called components. You use each vector’s coordinates to find their magnitudes and combined dot product. If your math problem already gives the vectors’ magnitudes, skip the magnitude step below. For example, find the angle between vector u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} and vector v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}. Vector u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} has coordinates at (2, 2) and vector v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}} has coordinates at (0, 3). Sometimes, vectors are written as u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} = 2i + 2j and v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}} = 0i + 3j. While our example uses two-dimensional vectors, finding the angle between 3-dimensional vectors follows the same steps.
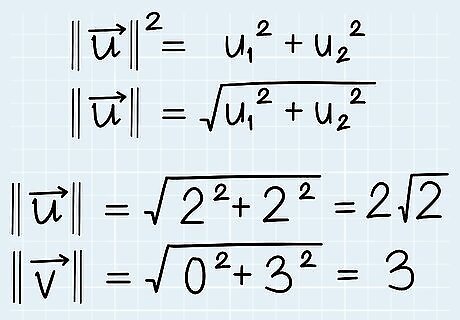
Calculate the magnitude of each vector. Picture a right triangle drawn from the vector's x-component, its y-component, and the vector itself. The vector forms the hypotenuse of the triangle, so to find its magnitude, simply use the Pythagorean theorem. Just plug each vector’s coordinates into the theorem. In the Pythagorean theorem of a + b + c, the vector’s magnitude is denoted by c. So, just rewrite the equation to isolate the magnitude on one side: ||u|| = √(u1 + u2) with u1 + u2 being the vector’s x and y coordinates. Using our example, find the magnitudes for vector u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} at (2, 2) and vector v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}} at (0, 3). Insert u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} coordinates into the theorem: √2 + 2 = √8 = 2√2. So, ||u|| = 2√2. Find v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}} magnitude: √0 + 3 = √9. So, || v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}|| = 3. If a vector is 3-dimensional or has more than 2 components, simply continue adding +u3 + u4 + … to the Pythagorean Theorem.
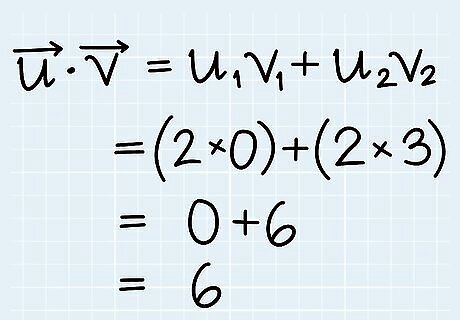
Calculate the dot product of the 2 vectors. The dot product is a way to multiply vectors, which is also commonly called the scalar product. To calculate the dot product, multiply the same direction coordinates of the vectors, then add the results together. For computer graphics programs, see Tips before you continue. Defining Dot ProductIn mathematical terms, u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} • v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}} = u1v1 + u2v2, where (u1, u2) are the coordinates for vector u. If your vector has more than 2 components, simply continue to add + u3v3 + u4v4... Using our example, u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} = (2, 2) and v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}} = (0, 3). Find u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} • v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}. Multiply the x-coordinates of u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} and v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}} and the y-coordinates. uxvx + uyvy = (2)(0) + (2)(3) = 0 + 6 = 6. 6 is the dot product of vector u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} and v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}.
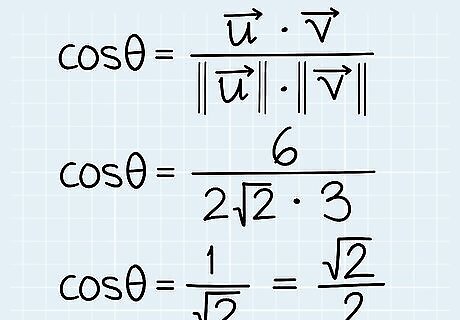
Plug the dot product and each vector’s magnitude into the formula. Remember, the formula is θ = c o s − 1 {\displaystyle \theta =cos^{-1}} {\displaystyle \theta =cos^{-1}} ( u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} • v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}) / (|| u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}}|| || v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}||) Now that you know both the dot product and the magnitudes of each vector, simply enter them into this formula.Finding Cosine with Dot Product and MagnitudeIn our example, θ = cos6 / (2√2•3). Simplify to get θ = cos(√2 / 2).
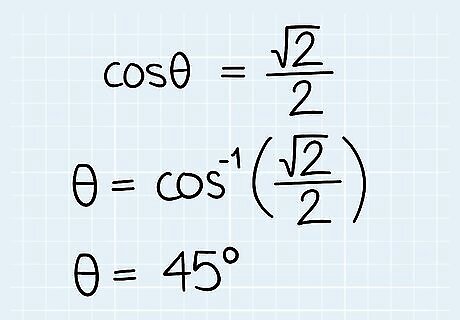
Use a scientific calculator to find the angle based on the cosine. On most calculators, use either the arccos or cos function on your calculator to find the angle θ. Simply enter “arccos” and the dot product divided by the vectors’ magnitudes. For some results, use the unit circle to work out the angle.Finding an Angle with CosineIn our example, θ = cos(√2 / 2). Enter "arccos(√2 / 2)" in your calculator to get θ = 45º. Alternatively, find the angle θ on the unit circle where cosθ = √2 / 2.
Using the Cross Product Formula
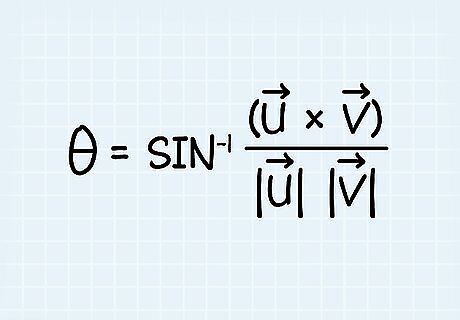
Use the formula: θ = s i n − 1 {\displaystyle \theta =sin^{-1}} {\displaystyle \theta =sin^{-1}} ( u → x {\displaystyle {\overrightarrow {u}}x} {\displaystyle {\overrightarrow {u}}x} v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}) / (|| u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}}|| || v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}||). This formula uses sine and the cross product of vectors to find the angle between them. Unlike the dot product formula, which gives you a scalar answer, the cross product formula gives you an answer as a vector. In this formula: θ {\displaystyle \theta } \theta is the angle between the vectors. s i n − 1 {\displaystyle sin^{-1}} sin^{{-1}} is the inverse of sine, or the arc sin. u → x {\displaystyle {\overrightarrow {u}}x} {\displaystyle {\overrightarrow {u}}x} v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}} is the cross product of vector u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} and v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}. || u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}}|| || v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}|| is the magnitude of vector u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} and v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}.
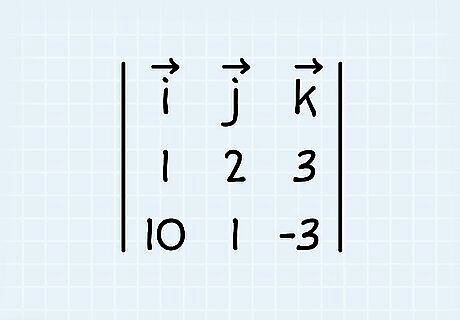
Find the cross product using the vectors’ coordinates. In most math problems, you have the dimensional coordinates, or components, of each vector written as i + j + k {\displaystyle i+j+k} {\displaystyle i+j+k}. To find the cross product, make a matrix with the first vector’s coordinates in the first row and the second vector’s coordinates in the second row. Calculate the i, j, and k values for each matrix section. For example, find the angle between 2 vectors where u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} is 1i - 2j + 3k and v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}} is 10i + 1j - 3k. Draw a matrix for u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} and v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}: 1 2 3 is on the top row, and 10 1 -3 is on the bottom row. Solve the matrix for i: i = (uj * vk) - (vj * uk) i = (6 - 3) = 3 Solve the matrix for j: j = (ui * vk) - (vi * uk)j = (-3 - 30) = -33 Solve the matrix for k: k = (ui * vj) - (vi * uj)k = (1 - -20) = 21 Find the coordinates for i - j + k: 3i - -33j + 21k = 3i + 33j + 21k or <3, 33, 21>
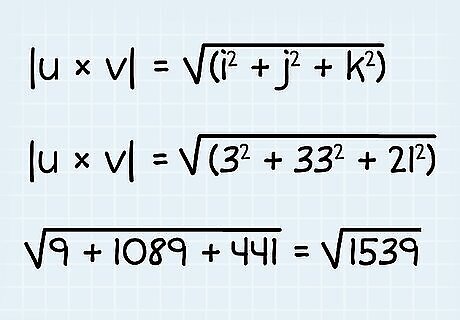
Calculate the magnitude of the cross product. The final step in finding the cross product of vectors is finding the magnitude of their coordinates. Remember, use the Pythagorean Theorem to find a vector’s magnitude. Just plug in the i, k, j coordinates of the cross product of the vectors to get their magnitude. The cross product of u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} x v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}} is 3i + 33j + 21k or <3, 33, 21>. Use the Pythagorean Theorem to find the magnitude: ||u x v|| = √(i + j + k) Plug in 3i + 33j + 21k into the theorem: √((3) + (33) + (21)) Solve: √9 + 1089 + 441 = √1539 The cross product of vector u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} x v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}} = √1539
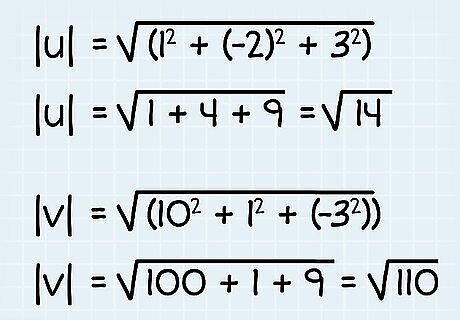
Find the magnitude of each vector. Now, calculate the magnitude of each vector using their dimensional coordinates. Just plug the coordinates into the Pythagorean Theorem like in the step above. In the example, u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}} is 1i - 2j + 3k and v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}} is 10i + 1j - 3k. Find the magnitude of u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}}: ||u|| = √i + j + k = √((1) + (-2) + (3)) = √1 + 4 + 9 = √14 Find the magnitude of v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}: ||v|| = √((10) + (1) + (-3)) = √100 + 1 + 9 = √110
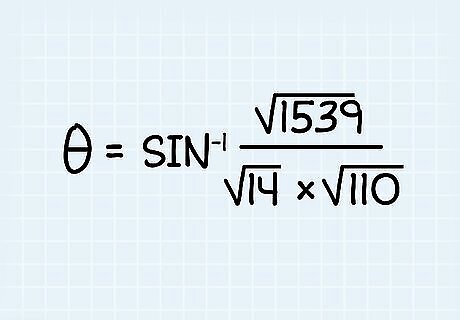
Plug the cross product and the vectors’ magnitude into the formula. Now that you have the vectors’ cross product and magnitudes, simply enter them into the formula θ = s i n − 1 {\displaystyle \theta =sin^{-1}} {\displaystyle \theta =sin^{-1}} ( u → x {\displaystyle {\overrightarrow {u}}x} {\displaystyle {\overrightarrow {u}}x} v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}) / (|| u → {\displaystyle {\overrightarrow {u}}} {\overrightarrow {u}}|| || v → {\displaystyle {\overrightarrow {v}}} {\overrightarrow {v}}||). In our example, θ = sin(√1539 / √14 * √110)

Find the angle using a calculator. Simply take the inverse sine of the cross product and magnitudes to find the angle between the vectors. Using your calculator, find the arcsin or sin function. Then, enter in the cross product and magnitude. In our example, enter “arcsin(√1539 / √14 * √110) into your calculator to get θ = 88.5º.
Understanding the Dot Product Formula
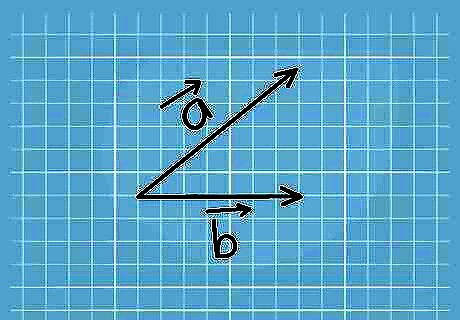
Understand the purpose of the angle formula. This formula was not derived from existing rules. Instead, it was created as a definition of 2 vectors' dot product and the angle between them. However, this decision was not arbitrary. With a look back to basic geometry, you see why this formula results in intuitive and useful definitions. The examples below use 2-dimensional vectors because these are the most intuitive to use. Vectors with 3 or more components use the same formula.
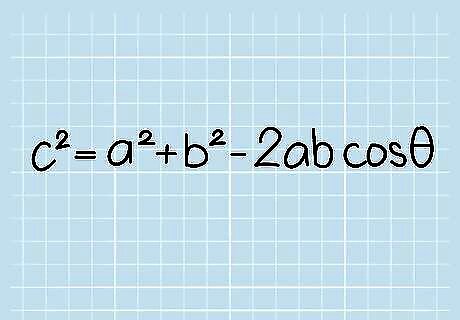
Review the Law of Cosines used in the formula. Take an ordinary triangle, with angle θ between sides a and b, and opposite side c. The Law of Cosines states that c = a + b -2abcos(θ). This is derived fairly easily from basic geometry.
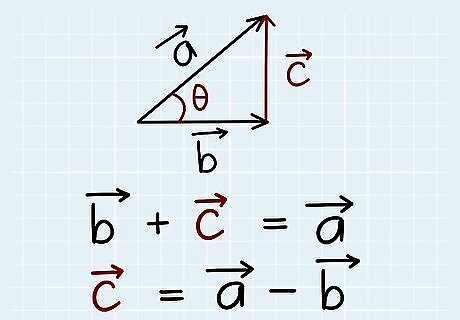
Connect 2 vectors to form a triangle. Sketch a pair of 2D vectors on paper, vectors a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} and b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}}, with angle θ between them. Draw a third vector between them to make a triangle. In other words, draw vector c → {\displaystyle {\overrightarrow {c}}} {\overrightarrow {c}} such that b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}} + c → {\displaystyle {\overrightarrow {c}}} {\overrightarrow {c}} = a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}}. This vector c → {\displaystyle {\overrightarrow {c}}} {\overrightarrow {c}} = a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} - b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}}.
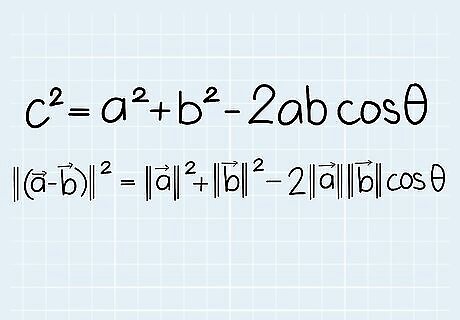
Write the Law of Cosines for the triangle. Insert the length of the "vector triangle" sides in our example into the Law of Cosines: ||(a - b)|| = ||a|| + ||b|| - 2||a|| ||b||cos(θ)
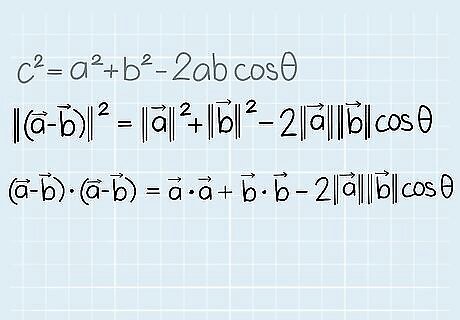
Write the Law of Cosines using the dot product of vector a and b. Remember, the dot product is the magnification of 1 vector projected onto another. A vector's dot product with itself doesn't require any projection, since there is no difference in direction. This means that a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} • a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} = ||a||. Use this fact to rewrite the equation: ( a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} - b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}}) • ( a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} - b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}}) = a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} • a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} + b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}} • b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}} - 2||a|| ||b||cos(θ)

Rewrite the dot product into the angle formula. Expand the left side of the formula, then simplify to reach the formula used to find angles. a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} • a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} - a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} • b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}} - b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}} • a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} + b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}} • b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}} = a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} • a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} + b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}} • b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}} - 2||a|| ||b||cos(θ) - a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} • b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}} - b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}} • a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} = -2||a|| ||b||cos(θ) -2( a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} • b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}}) = -2||a|| ||b||cos(θ) a → {\displaystyle {\overrightarrow {a}}} {\overrightarrow {a}} • b → {\displaystyle {\overrightarrow {b}}} {\overrightarrow {b}} = ||a|| ||b||cos(θ)






















Comments
0 comment