
views
Calculating Powerball Jackpot Odds

Understand the calculations involved. To find the odds of winning any lottery, divide the number of winning lottery numbers by the total number of possible lottery numbers. If the numbers are chosen from a set and the order of the numbers doesn't matter, use the formula n ! r ! ( n − r ) ! {\displaystyle {\frac {n!}{r!(n-r)!}}} {\frac {n!}{r!(n-r)!}}. In the formula, n stands for the total number of possible numbers and r stands for the number of numbers chosen. The "!" denotes a factorial, which for any integer n is n*(n-1)*(n-2)...and so on until 0 is reached. For example, 3! represents 3 × 2 × 1 {\displaystyle 3\times 2\times 1} 3\times 2\times 1. For a simple example, imagine you have to choose two numbers and you can pick numbers from 1 to 5. Your odds of choosing the two "correct" numbers (the winning numbers) would be defined as 5 ! 2 ! × 3 ! {\displaystyle {\frac {5!}{2!\times 3!}}} {\frac {5!}{2!\times 3!}}. This would then be solved as 5 × 4 × 3 × 2 × 1 2 × 1 × 3 × 2 × 1 {\displaystyle {\frac {5\times 4\times 3\times 2\times 1}{2\times 1\times 3\times 2\times 1}}} {\frac {5\times 4\times 3\times 2\times 1}{2\times 1\times 3\times 2\times 1}}, which is 120 ÷ 12 {\displaystyle 120\div 12} 120\div 12, or 10. So, your odds of winning this game are 1 in 10. Factorial calculations can get unwieldy, especially with large numbers. Most calculators have a factorial function to ease your calculations. Alternately, you can type the factorial into Google (as "55!" for example) and it will solve it for you.
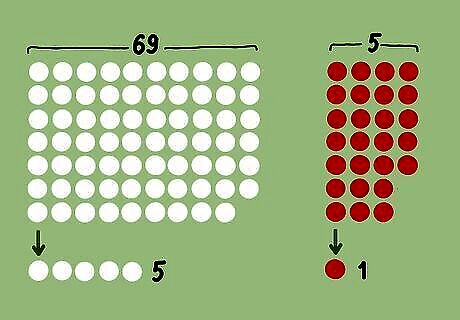
Establish the lottery's rules. The majority of Mega Millions, Powerball, and other large lotteries use roughly the same rules: 5 or 6 numbers are chosen from a large pool of numbers in no particular order. Numbers may not be repeated. In some games, a final number is chosen from a smaller set of numbers (the "Powerball" in Powerball games is an example). In Powerball, 5 numbers are chosen from 69 possible numbers. Then, for the single Powerball, one number is chosen from a set of 26 possible numbers. Other games may have you choose 5 or 6 numbers, or more, from a larger or smaller pool of numbers. To calculate the odds of winning, you simply need to know the number of winning numbers and the total number of possible numbers.
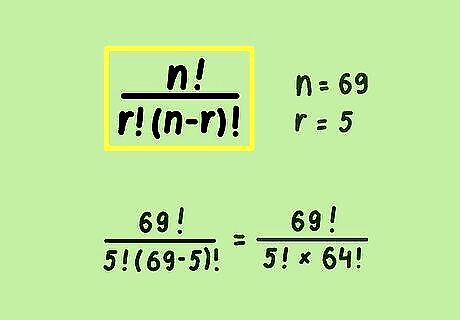
Input the numbers into the probability equation. The first part of Powerball odds determines the number of ways 5 numbers could be chosen out of 69 unique numbers. Using Powerball rules, the completed equation for the first 5 numbers would be: 69 ! 5 ! ( 69 − 5 ) ! {\displaystyle {\frac {69!}{5!(69-5)!}}} {\frac {69!}{5!(69-5)!}}, which simplifies to 69 ! 5 ! × 64 ! {\displaystyle {\frac {69!}{5!\times 64!}}} {\frac {69!}{5!\times 64!}}.
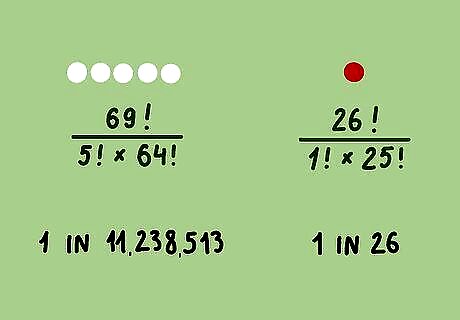
Calculate your odds of choosing correctly. Solving this equation is best done entirely in a search engine or calculator, as the numbers involved are inconvenient to write down between steps. The result tells you there are 11,238,513 possible combinations of 5 numbers in a set of 69 unique numbers. This means that you have a 1 in 11,238,513 chance of choosing the five numbers correctly. To calculate your odds of choosing the final Powerball correctly, you would complete the same equation using the values for the Powerball (1 number out of 26 possible numbers). Since you're only picking 1 number here, you don't necessarily have to complete the entire equation. The answer will be 26 because there are 26 different ways 1 number can be chosen from a set of 26 unique numbers.
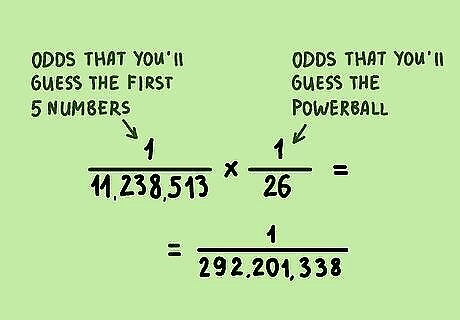
Multiply to calculate your odds of winning the jackpot. To calculate the odds that you'll guess the first 5 numbers and the Powerball correctly to win the jackpot, multiply the odds that you'll guess the first 5 numbers (1 in 11,238,513) by the odds that you'll guess the Powerball correctly (1 in 26). Your equation would be 1 11 , 238 , 513 × 1 26 {\displaystyle {\frac {1}{11,238,513}}\times {\frac {1}{26}}} {\displaystyle {\frac {1}{11,238,513}}\times {\frac {1}{26}}}. So, your odds of choosing the first five numbers and the Powerball correctly and winning the jackpot are 1 in 292,201,338.
Determining Lesser Prize Odds
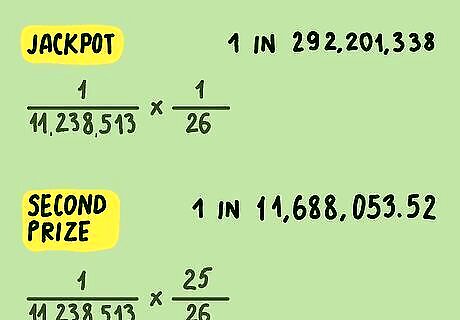
Calculate your odds of winning the second prize. To return to the Powerball game, you have 5 numbers and a single Powerball. If you guess all 5 of the other numbers correctly but don't get the Powerball, you'll win the second prize. If you calculated your odds of winning the jackpot, you already know that your odds of guessing all 5 numbers correctly are 1 in 11,238,513. To win the second prize, you would have to guess the Powerball incorrectly. If you calculated your odds of winning the jackpot, you know that your odds of guessing the Powerball correctly are 1 in 26. Therefore, your odds of guessing the Powerball incorrectly are 25 in 26. Use the same equation with these values to determine your odds of winning the second prize: 1 11 , 238 , 513 × 25 26 {\displaystyle {\frac {1}{11,238,513}}\times {\frac {25}{26}}} {\displaystyle {\frac {1}{11,238,513}}\times {\frac {25}{26}}}. When you complete this calculation, you'll see that your odds of winning the second prize are 1 in 11,688,053.52.
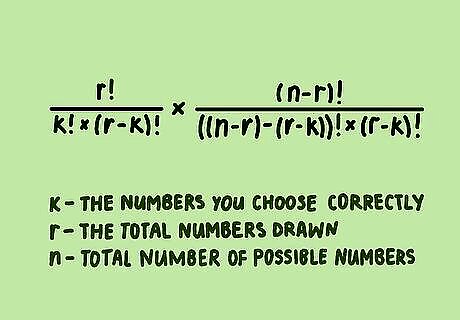
Use an expanded equation to find your odds for other prizes. To win other prizes, you guess some, but not all, of the winning numbers correctly. To figure out your odds, use an equation in which "k" represents the numbers you choose correctly, "r" represents the total numbers drawn, and "n" represents the number of unique numbers the numbers will be drawn from. Without numbers, the formula looks like this: r ! k ! × ( r − k ) ! × ( n − r ) ! ( ( n − r ) − ( r − k ) ) ! × ( r − k ) ! {\displaystyle {\frac {r!}{k!\times (r-k)!}}\times {\frac {(n-r)!}{((n-r)-(r-k))!\times (r-k)!}}} {\displaystyle {\frac {r!}{k!\times (r-k)!}}\times {\frac {(n-r)!}{((n-r)-(r-k))!\times (r-k)!}}}. For example, you might use the Powerball values to determine your odds of correctly guessing 3 of the 5 chosen numbers from the set of 69 unique numbers. Your equation would look like this: 5 ! 3 ! × ( 5 − 3 ) ! × ( 69 − 5 ) ! ( ( 69 − 5 ) − ( 5 − 3 ) ) ! × ( 5 − 3 ) ! {\displaystyle {\frac {5!}{3!\times (5-3)!}}\times {\frac {(69-5)!}{((69-5)-(5-3))!\times (5-3)!}}} {\displaystyle {\frac {5!}{3!\times (5-3)!}}\times {\frac {(69-5)!}{((69-5)-(5-3))!\times (5-3)!}}} The result of this equation tells you the number of ways that 3 numbers can be chosen correctly out of 5 numbers. Your odds will be that number out of the total number of ways 5 numbers can be chosen correctly.
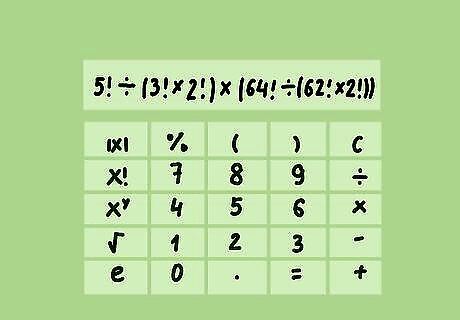
Solve your equation to find the odds of correctly guessing the numbers. Just as with the base equation, this equation is best solved by typing the entire thing into a calculator or search engine. Some intermediate numbers involved in the calculation would be cumbersome to write down and it would be easy to make a mistake. In the previous example, your odds of guessing 3 of the 5 chosen numbers in Powerball would be 20,160 in 11,238,513.

Multiply the result by the Powerball value to determine your odds of winning that prize. While this formula gives you the odds of guessing only some of the numbers correctly, you still haven't factored in the Powerball. To find your true odds, multiply the result by your odds of getting the Powerball number correct or incorrect (whichever value you want to find). For example, if you wanted to calculate your odds for getting only 3 of the 5 numbers correct and getting the Powerball incorrect, your equation would be 20 , 160 11 , 238 , 513 × 25 26 {\displaystyle {\frac {20,160}{11,238,513}}\times {\frac {25}{26}}} {\displaystyle {\frac {20,160}{11,238,513}}\times {\frac {25}{26}}}, or 1 in 579.76. On the other hand, your odds for getting 3 of the 5 numbers correct and getting the Powerball correct would be 20 , 160 11 , 238 , 513 × 1 26 {\displaystyle {\frac {20,160}{11,238,513}}\times {\frac {1}{26}}} {\displaystyle {\frac {20,160}{11,238,513}}\times {\frac {1}{26}}}, or 1 in 14,494.11.
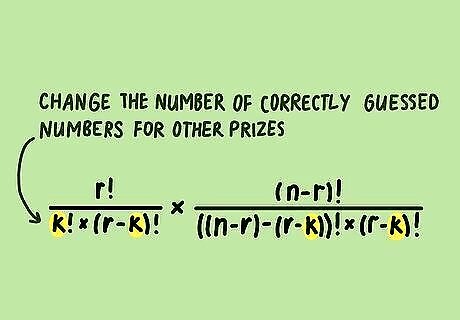
Change the number of correctly guessed numbers for other prizes. Once you have the formula down, simply change the value of "k" to find the odds of winning different levels of prizes. Generally, your odds of winning will decrease as the value of "k" increases. If you're calculating odds for Powerball or a similar game, don't forget to multiply your result by the Powerball value.
Calculating Other Lotto Odds

Find the expected return of a lottery ticket. The expected return tells you what you could theoretically expect to get back in return for buying a single lottery ticket. To calculate the expected return of a single ticket, multiply the odds of a particular payout by the value of that payout. If you did this with every possible prize you could win, you would get a range of expected returns. To return to the Powerball example, the expected return of a single $2 ticket would be around $1.79 at the high end and as little as $1.35 at the low end. Keep in mind that "expected return" is a term of art used in statistics. Your actual payout will almost always be much less than the expected return you calculate.

Compare the cost of a single ticket to its expected return. You can determine the expected benefit of playing the lottery by comparing the expected return of a ticket to the cost of a ticket. Most of the time, the expected return will be lower than the cost of the ticket. Additionally, your actual return will likely differ greatly from the expected value. You'll typically only get a fraction of the expected value, if anything at all. Calculating the odds can help you determine which lottery games have the best expected benefit. For example, at one time, the New York Lottery had a $1 Take Five ticket with an expected value that equaled its cost. If you played this game, you could expect to break even over time.
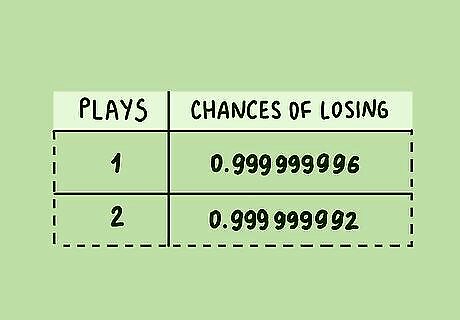
Determine the increase in odds from playing multiple times. Playing the lottery multiple times increases your overall odds of winning, however slightly. It's easier to envision this increase as a decrease in your chance of losing. For example, if your overall chances of winning are 1 in 250,000,000, your chances of losing on one play are 249 , 999 , 999 ÷ 250 , 000 , 000 {\displaystyle 249,999,999\div 250,000,000} 249,999,999\div 250,000,000, which is equal to a number very close to 1 (0.99999...). If you play twice, that number is squared ( ( 249 , 999 , 999 ÷ 250 , 000 , 000 ) 2 {\displaystyle (249,999,999\div 250,000,000)^{2}} (249,999,999\div 250,000,000)^{{2}}), representing a movement slightly away from 1 (and therefore a better chance of winning).

Find the number of plays needed for decent odds of winning. Most lottery players are convinced that if they play often enough, they will significantly increase their chances of winning. It is true that playing more increases your odds of winning. However, it takes a long time for that increased chance to become significant. For example, if you had a 1 in 250,000,000 chance of winning on one play, it would take roughly 180 million plays to reach 50-50 odds of winning. At this rate, if you bought ten tickets a day for 49,300 years, you would have a 50 percent chance of winning. Additionally, if you finally reached 50-50 odds, you still wouldn't be guaranteed a win if you bought two tickets on that day. Your overall odds of winning would still remain roughly 50% for each of those tickets.











Comments
0 comment