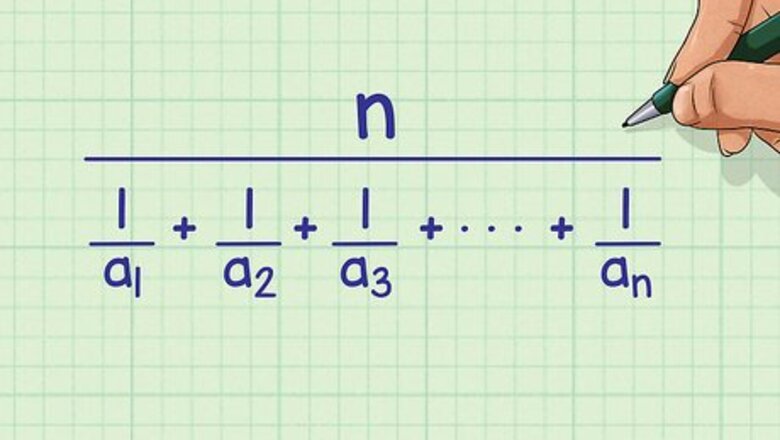
views
Setting Up the Formula
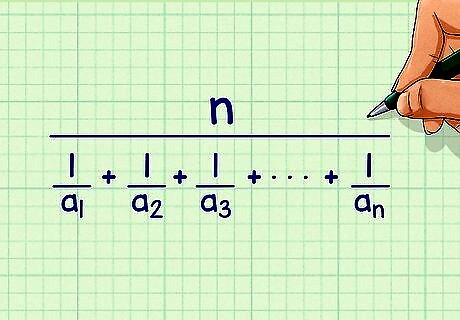
Set up the formula for the harmonic mean. The formula is n 1 a 1 + 1 a 2 + 1 a 3 + . . . + 1 a n {\displaystyle {\frac {n}{{\frac {1}{a_{1}}}+{\frac {1}{a_{2}}}+{\frac {1}{a_{3}}}+...+{\frac {1}{a_{n}}}}}} {\frac {n}{{\frac {1}{a_{{1}}}}+{\frac {1}{a_{{2}}}}+{\frac {1}{a_{{3}}}}+...+{\frac {1}{a_{{n}}}}}}, where n {\displaystyle n} n is the number of values in the set of numbers, and a 1 {\displaystyle a_{1}} a_{{1}}, a 2 {\displaystyle a_{2}} a_{{2}}, a 3 . . . {\displaystyle a_{3}...} a_{{3}}... are the values in the set.
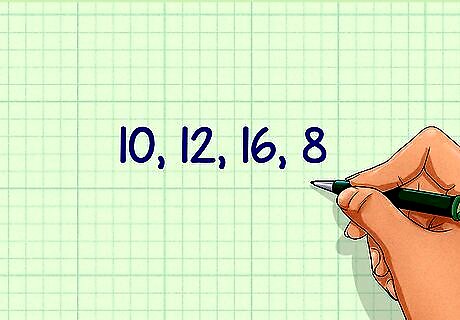
Determine the values you need to find the harmonic mean for. This can be any set of numbers. For example, you may need to find the harmonic mean for the numbers 10, 12, 16, and 8.
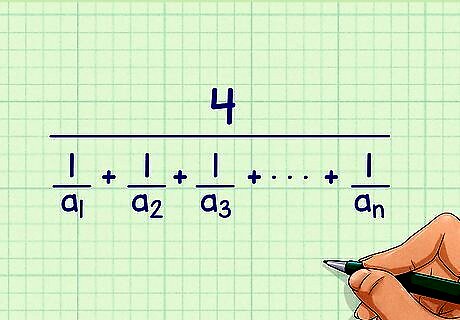
Plug the value of n {\displaystyle n} n into the formula. This will equal the number of values in your set. For example, if you are finding the harmonic mean of the numbers 10, 12, 16, and 8, you are working with 4 values, the numerator of your formula will be 4: 4 1 a 1 + 1 a 2 + 1 a 3 + . . . + 1 a n {\displaystyle {\frac {4}{{\frac {1}{a_{1}}}+{\frac {1}{a_{2}}}+{\frac {1}{a_{3}}}+...+{\frac {1}{a_{n}}}}}} {\frac {4}{{\frac {1}{a_{{1}}}}+{\frac {1}{a_{{2}}}}+{\frac {1}{a_{{3}}}}+...+{\frac {1}{a_{{n}}}}}}
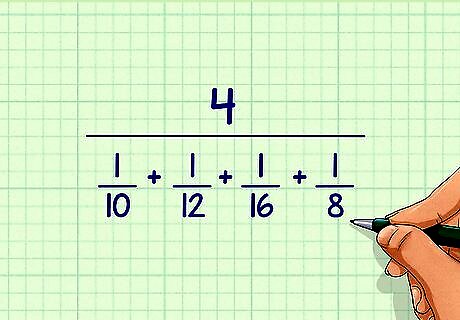
Plug the values your are averaging into your formula. You will take the reciprocal of each number and add them in the denominator of the formula. Remember, when you take the reciprocal of a whole number, you turn the number into a fraction by placing a 1 in the numerator and the whole number in the denominator. For example, if the values in your set are 10, 12, 16, and 8, you would place the fractions 1 10 {\displaystyle {\frac {1}{10}}} {\frac {1}{10}}, 1 12 {\displaystyle {\frac {1}{12}}} {\frac {1}{12}}, 1 16 {\displaystyle {\frac {1}{16}}} {\frac {1}{16}}, 1 8 {\displaystyle {\frac {1}{8}}} {\frac {1}{8}} in your denominator: 4 1 10 + 1 12 + 1 16 + 1 8 {\displaystyle {\frac {4}{{\frac {1}{10}}+{\frac {1}{12}}+{\frac {1}{16}}+{\frac {1}{8}}}}} {\frac {4}{{\frac {1}{10}}+{\frac {1}{12}}+{\frac {1}{16}}+{\frac {1}{8}}}}
Calculating the Harmonic Mean by Hand or Calculator
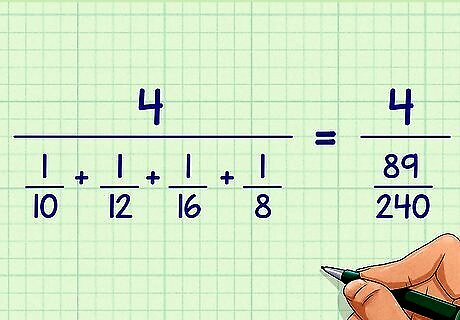
Add the fractions in the denominator. You can use a calculator, or add them up by hand. If you are not using a calculator, remember to find a common denominator first. To learn more about adding fractions, read Add Fractions. For example: 4 1 10 + 1 12 + 1 16 + 1 8 = 4 89 240 {\displaystyle {\frac {4}{{\frac {1}{10}}+{\frac {1}{12}}+{\frac {1}{16}}+{\frac {1}{8}}}}={\frac {4}{\frac {89}{240}}}} {\frac {4}{{\frac {1}{10}}+{\frac {1}{12}}+{\frac {1}{16}}+{\frac {1}{8}}}}={\frac {4}{{\frac {89}{240}}}}
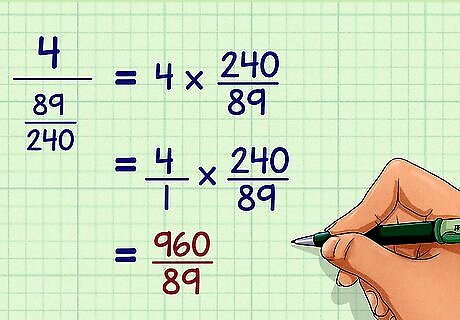
Divide the numerator by the denominator. Remember that dividing by a fraction is the same as multiplying by its reciprocal. For example: 4 89 240 {\displaystyle {\frac {4}{\frac {89}{240}}}} {\frac {4}{{\frac {89}{240}}}} = 4 × 240 89 {\displaystyle =4\times {\frac {240}{89}}} =4\times {\frac {240}{89}} = 4 1 × 240 89 {\displaystyle ={\frac {4}{1}}\times {\frac {240}{89}}} ={\frac {4}{1}}\times {\frac {240}{89}} = 960 89 {\displaystyle ={\frac {960}{89}}} ={\frac {960}{89}}
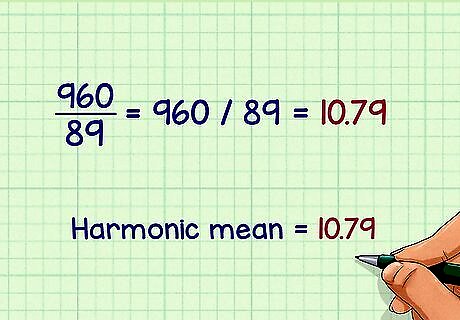
Convert to a decimal to find the harmonic mean of your set of numbers. To convert a fraction to a decimal, divide the numerator by the denominator. For example: 960 89 {\displaystyle {\frac {960}{89}}} {\frac {960}{89}} = 960 ÷ 89 {\displaystyle =960\div 89} =960\div 89 = 10.79 {\displaystyle =10.79} =10.79So, the harmonic mean of the numbers 10, 12, 16, and 8 is 10.79.
Calculating the Harmonic Mean using Excel
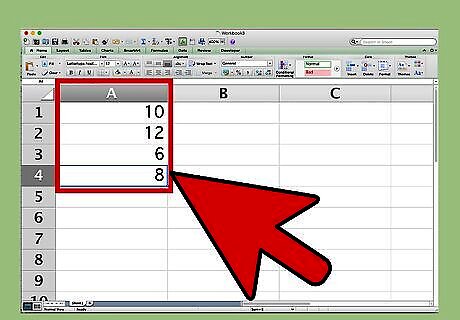
Enter the values into your spreadsheet. Make sure to only place one value in each cell. For example, if you need to find the harmonic mean of 10, 12, 16, and 8, you might type each of these values into a separate cell in the spreadsheet, cells A1-A4.
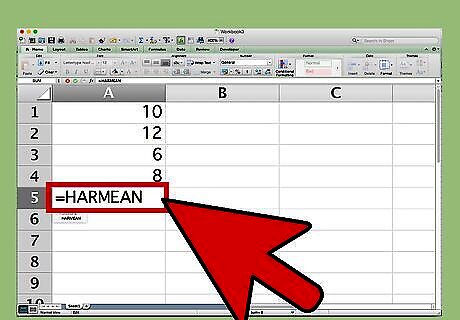
Enter the function for the harmonic mean. The function is HARMEAN(number 1, [number 2]...). To select the function, begin typing “=HARMEAN” into a blank cell of the spreadsheet, then double-click on the function when it pops up. For example, type “=HARMEAN” into cell A5 of your spreadsheet and double-click on the function.
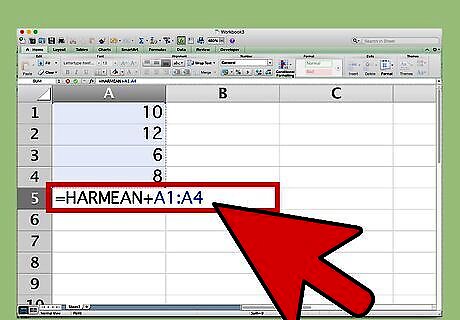
Highlight the cells containing the values you are averaging. Hit the enter key. Excel will calculate the harmonic mean for you and display it in the spreadsheet. For example, highlight cells A1-A4 of your spreadsheet and hit enter. Excel will calculate 10.78652 as the harmonic mean.
















Comments
0 comment