How to Work out Compound Interest on Savings

Gathering Your Variables

Determine your principal balance. The "principal" is the current or starting amount of money in the savings account you are calculating interest for. For example, if you put $1,000 into a new savings account today, your principal would be $1,000. If you have an existing savings account, the principal is the amount of money in the account as of your last account statement. For an existing savings account, log into online banking, check your latest account statement, or contact your bank to determine the current amount in your account.

Identify your annual interest rate. Your annual interest rate is the percentage of the account balance that is paid out in interest each year. This number is also referred to as the annual percentage rate (APR) in financial documents. It will be stated on your savings account agreement. For example, a savings account might have an APR of 1.2 percent. Deposit accounts, like certificates of deposits (CDs), use another term, annual percentage yield (APY), to refer to the annual rate. Make sure you are using the annual rate (the amount of interest paid each year) and not the periodic rate (the amount of interest paid each time the interest compounds each year). For example, an account with interest that compounds quarterly (four times per year) might have a periodic interest rate of 0.3 percent, but an annual rate of 1.2 percent. Remember to use the annual rate in your calculations. For the purpose of calculating compound interest, your rate must be in decimal form. Convert it by dividing your started interest rate by 100. For example, 1 percent would be 1/100, or 0.01.

Figure out your compounding frequency. Standard savings accounts are compounded either monthly, quarterly or yearly. This means that the interest on the account is calculated and paid twelve or four times per year, respectively. Other accounts may be calculated daily, weekly, semiannually, or annually. Look through your account agreement and determine how many times per year the interest is compounded. You will use this number in your calculations for the "compounding frequency." Specifically, use the following numbers: For annual compounding, use 1 (once per year). For semiannual, use 2 (twice per year). For quarterly, use 4. For monthly, use 12. For weekly, use 52. For daily, use 365.

Determine the time period. Decide how long a time period you will use in your interest calculation. Compound interest works better over long periods of time, as the amount of interest earned increases over time with the account balance. Whatever you decide, express your time period in years when performing your calculations.

Decide whether or not you will be making regular contributions. You can also calculate compound interest on an account to which you will be making regular additions. For example, if you started a savings account with $1,000, you may also want to save a bit each month, maybe $100, and add that to the account. The regular contributions will increase both the account value and the amount of interest earned. If you are calculating interest for an account to which you will be making regular contributions, use the part of this article titled "Calculating Compound Interest with Regular Contributions."

Calculating Compound Interest on Savings

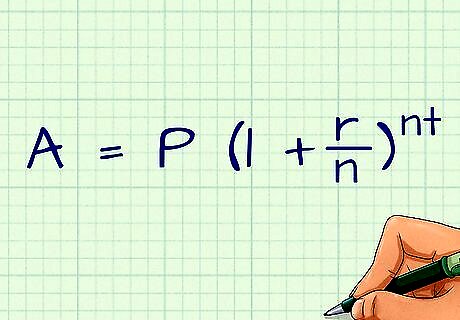
Learn the compound interest formula. The compound interest formula is typically expressed as A = P ( 1 + r n ) n t {\displaystyle A=P(1+{\frac {r}{n}})^{nt}} A=P(1+{\frac {r}{n}})^{{nt}}. In the formula, the variables stand for the following values: A is the final value of the account after interest is calculated. P is the principal in the account. r is the annual interest rate. n is the compounding frequency. t is the time period in years.

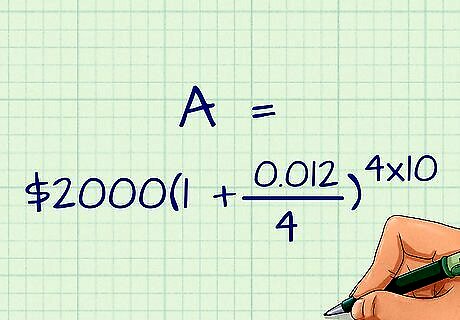
Input your variables. Place your savings account information in the formula in the appropriate places. Remember to format each one correctly. Make sure that the time, t, is in years and that the interest rate, r, is in decimal form. For example, imagine you start a new savings account with a $2,000 (P=$2,000) deposit. The account will earn 1.2 percent interest (r=0.012) compounded quarterly (n=4). You decide to leave the money in the account for ten years (t=10). Using the example savings account, your completed equation would look like this: A = $ 2 , 000 ( 1 + 0.012 4 ) 4 ∗ 10 {\displaystyle A=\$2,000(1+{\frac {0.012}{4}})^{4*10}} A=\$2,000(1+{\frac {0.012}{4}})^{{4*10}}

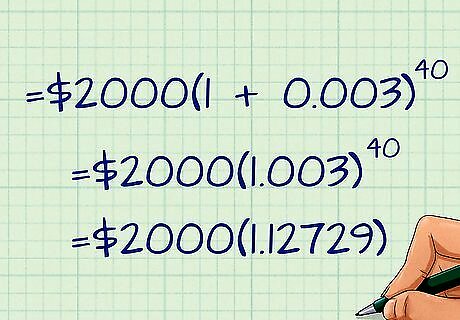
Solve the equation. Begin solving the equation by simplifying the parts of the equation involving your compounding frequency, n. That is, solve the figures r n {\displaystyle {\frac {r}{n}}} {\frac {r}{n}} and n t {\displaystyle nt} nt first. For the example, equation, these calculations would result in the following: A = $ 2 , 000 ( 1 + 0.003 ) 40 {\displaystyle A=\$2,000(1+0.003)^{40}} A=\$2,000(1+0.003)^{{40}}. Next, solve the addition in parentheses. For the example, this would give: A = $ 2 , 000 ( 1.003 ) 40 {\displaystyle A=\$2,000(1.003)^{40}} A=\$2,000(1.003)^{{40}}. Then, calculate the exponent. The number above the others, on the far right, is the exponent. Calculate this by inputting the lower value ((1.003) in the example), pressing the exponent button x y {\displaystyle x^{y}} x^{y} on your calculator, and then entering the exponent (40) and pressing enter. For the example, this would give: A = $ 2 , 000 ( 1.12729 ) {\displaystyle A=\$2,000(1.12729)} A=\$2,000(1.12729). This result, 1.12729, was rounded to five decimal places. For a more accurate answer, keep more decimal places in your calculation. Finally, multiply the two remaining numbers to get your future account balance, A. In the example, this would be $2,254.58. Your $2,000 deposit will be worth $2,254.58 in ten years if you put it into an account earning 1.2 percent annual interest compounded quarterly.

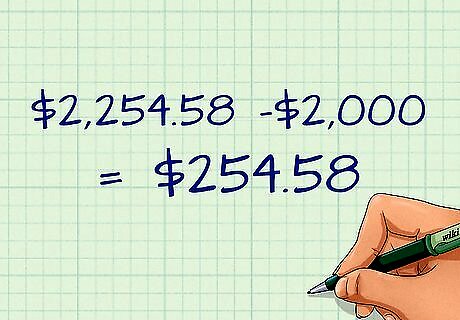
Calculate interest earned. Your interest earned is the amount that your account will increase over the specific time period. That is, it is is your final account balance, A, minus your original amount or principal (P). In the example, this would be $2,254.58 -$2,000, or $254.58. Your account will earn $254.58 in interest over the ten years.

Adjust your calculation as needed. Now that you've calculate interest for this account, do so for other accounts that may earn different interest or compound more or less frequently. Alternately, you can increase or reduce your principal amount or shorten or lengthen your time period. Changing these variables will allow you to compare your options and see what combinations will earn you the best return on your principal.

Calculating Compound Interest with Regular Contributions

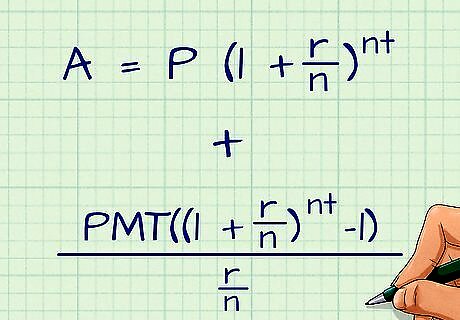
Understand the regular contributions formula. The regular contributions formula shows your the future value of an account earning compound interest that is also regularly increased with additional funds. It is the same formula used for calculating compound interest on a principal amount, plus an additional part for calculating compound interest on regular contributions. The formula is written out as the following: A = P ( 1 + r n ) n ∗ t + P M T ( ( 1 + r n ) n ∗ t − 1 ) r n {\displaystyle A=P(1+{\frac {r}{n}})^{n*t}+{\frac {PMT((1+{\frac {r}{n}})^{n*t}-1)}{\frac {r}{n}}}} A=P(1+{\frac {r}{n}})^{{n*t}}+{\frac {PMT((1+{\frac {r}{n}})^{{n*t}}-1)}{{\frac {r}{n}}}}. This formula is for regular contributions made at the end of the period in question (end of the month, end of the quarter, etc.). To calculate interest when payments are made at the beginning, add the figure, multiply the PMT part of the equation by 1 + r n {\displaystyle 1+{\frac {r}{n}}} 1+{\frac {r}{n}}. This formula only works if the payment frequency and compounding frequency are the same. For example, if you make monthly contributions, the interest compounds quarterly, this calculation will not be accurate.

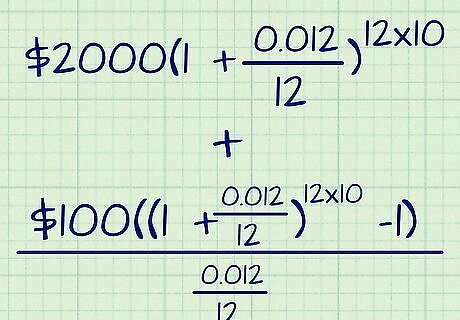
Fill out your equation. Imagine that you have a new savings account into which you just deposited $2,000. Your annual interest rate is 1.2 percent and interest compounds monthly. You plan to keep the money in the account for ten years. In addition, you plan to add $100 to the account at the end of each month over the entire 10 years. Your completed equation would be: A = $ 2 , 000 ( 1 + 0.012 12 ) 12 ∗ 10 + $ 100 ( ( 1 + 0.012 12 ) 12 ∗ 10 − 1 ) 0.012 12 {\displaystyle A=\$2,000(1+{\frac {0.012}{12}})^{12*10}+{\frac {\$100((1+{\frac {0.012}{12}})^{12*10}-1)}{\frac {0.012}{12}}}} A=\$2,000(1+{\frac {0.012}{12}})^{{12*10}}+{\frac {\$100((1+{\frac {0.012}{12}})^{{12*10}}-1)}{{\frac {0.012}{12}}}}.

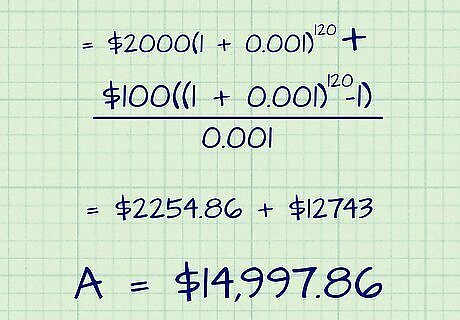
Do the math. Both parts of your equation (the principal and payment) will be solved in mostly the same way. Begin by simplifying the figures containing the compounding frequency, n. That is, multiply n times the time period in the exponents and divide the annual interest rate, r, by n inside the parentheses. Using the example equation, this would leave you with: A = $ 2 , 000 ( 1 + 0.001 ) 120 + $ 100 ( ( 1 + 0.001 ) 120 − 1 ) 0.001 {\displaystyle A=\$2,000(1+0.001)^{120}+{\frac {\$100((1+0.001)^{120}-1)}{0.001}}} A=\$2,000(1+0.001)^{{120}}+{\frac {\$100((1+0.001)^{{120}}-1)}{0.001}} Your next step is to add the numbers in parentheses (1+0.001 in the example), this gives you: A = $ 2 , 000 ( 1.001 ) 120 + $ 100 ( ( 1.001 ) 120 − 1 ) 0.001 {\displaystyle A=\$2,000(1.001)^{120}+{\frac {\$100((1.001)^{120}-1)}{0.001}}} A=\$2,000(1.001)^{{120}}+{\frac {\$100((1.001)^{{120}}-1)}{0.001}} After that, solve the exponents by raising the lower number (1.001) to the power of the higher number (120). This yields: A = $ 2 , 000 ( 1.12743 ) + $ 100 ( 1.12743 − 1 ) 0.001 {\displaystyle A=\$2,000(1.12743)+{\frac {\$100(1.12743-1)}{0.001}}} A=\$2,000(1.12743)+{\frac {\$100(1.12743-1)}{0.001}} Subtract the 1 in parentheses. The example equation is now: A = $ 2 , 000 ( 1.12743 ) + $ 100 ( 0.12743 ) 0.001 {\displaystyle A=\$2,000(1.12743)+{\frac {\$100(0.12743)}{0.001}}} A=\$2,000(1.12743)+{\frac {\$100(0.12743)}{0.001}} Multiply and divide the two parts separately. Multiply the principal and payments by the decimal figures in parentheses and then divide the payments side by the decimal underneath it. This results in: A = $ 2 , 254.86 + $ 12 , 743 {\displaystyle A=\$2,254.86+\$12,743} A=\$2,254.86+\$12,743 Add the final two numbers. Your result is the value of the account after your chosen time period. In the example, this is $14,997.86. Your 1.2 percent annual interest-earning account that compounds monthly will be worth $14,997.86 in ten years if you start with $2,000 in principal and add $100 each month.

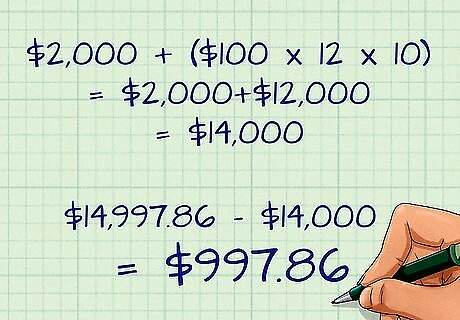
Calculate the interest earned. The interest earned on the account over the time period will be the value of the account after ten years minus the money you paid in. To find this number, first add up the money you paid in. This is your principal ($2,000 in the example), plus the sum of your contributions. In the example, this would be $2,000 plus ($100 per month)*(12 month per year)*(10 years), or $2,000+$12,000. Your paid-in amount would be $14,000. The interest earned is then $14,997.86 (the final account value) minus $14,000 (your paid-in amount), or $997.86. Your account will earn $997.86 in interest over the ten-year period.