Finding the Area of Any Quadrilateral: A Step-by-Step Guide

• Find the area of any quadrilateral by dividing it into 2 triangles. Then, find the area of each of those triangles using the formula ${\displaystyle A={\frac {1}{2}}bh}$ (Area = 1/2 base times height) and add them together.
• Use the formula ${\displaystyle A=lw}$ (Area = length times width) to find the area of a square or rectangle.
• Multiply the lengths of the 2 diagonal lines and divide by 2 to find the area of a rhombus or kite.
• Give the area of any quadrilateral in units squared. The unit corresponds with the unit used for the lengths you multiplied to find the area.

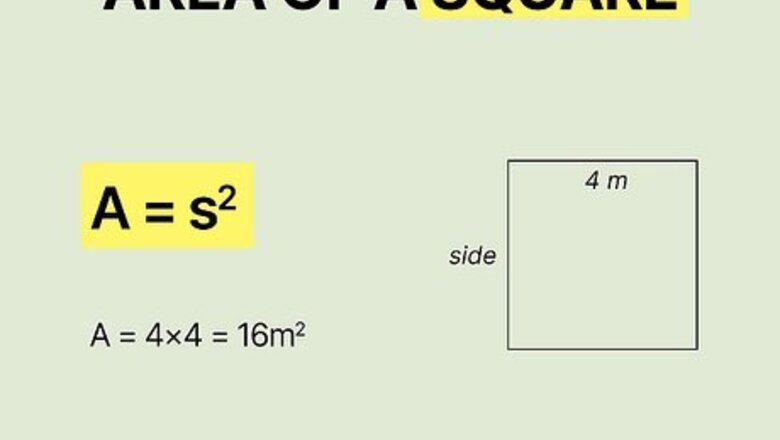
Square

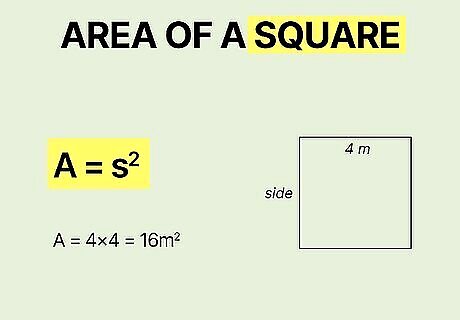
Use A = s 2 {\displaystyle A=s^{2}} {\displaystyle A=s^{2}} to find the area of a square. In the formula, "s" is the length of one side. Since all sides are equal, you only need the length of one of them to quickly find the area of any square. Then, express the area in units squared. For example, if you have a square and the length of one side is 4 m {\displaystyle 4m} {\displaystyle 4m}, you would multiply 4 ∗ 4 {\displaystyle 4*4} {\displaystyle 4*4} to get 16 m 2 {\displaystyle 16m^{2}} {\displaystyle 16m^{2}}. Try it with a square that has sides 2 i n {\displaystyle 2in} {\displaystyle 2in} long. Just multiply 2 ∗ 2 {\displaystyle 2*2} {\displaystyle 2*2}. That square has an area of 4 i n 2 {\displaystyle 4in^{2}} {\displaystyle 4in^{2}}. No matter what the unit is, it's always squared when you're talking about the area.

Rectangle

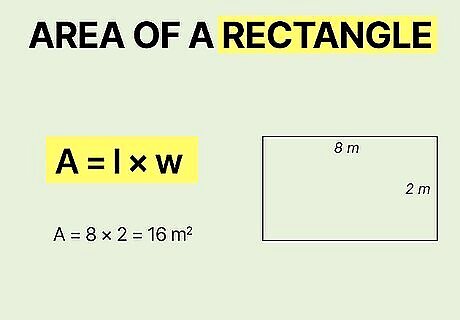
Use the formula A = l w {\displaystyle A=lw} A=lw to find the area of a rectangle. Since a rectangle has sides of 2 different lengths, you multiply one value by the other to find out how much space the rectangle covers. Just get the length of one of the short sides and one of the long sides. For example, if your rectangle has a length of 8 m {\displaystyle 8m} {\displaystyle 8m} and a width of 2 m {\displaystyle 2m} 2m, your equation would be A = 8 ∗ 2 {\displaystyle A=8*2} {\displaystyle A=8*2}, which gives you an answer of A = 16 m 2 {\displaystyle A=16m^{2}} {\displaystyle A=16m^{2}}. What if your rectangle has bigger numbers? The formula still works the same way. For example, a rectangle with a length of 1762 k m {\displaystyle 1762km} {\displaystyle 1762km} and a width of 288 k m {\displaystyle 288km} {\displaystyle 288km} would have an area of A = 1762 ∗ 288 = 507 , 456 k m 2 {\displaystyle A=1762*288=507,456km^{2}} {\displaystyle A=1762*288=507,456km^{2}}.

Parallelogram

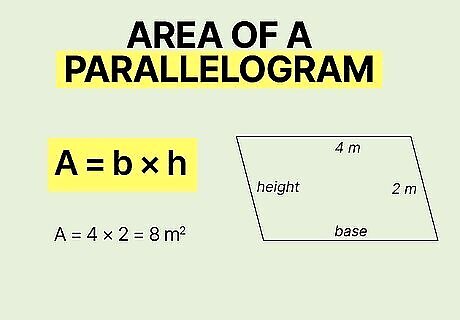
Find the area of a parallelogram with A = b h {\displaystyle A=bh} {\displaystyle A=bh}. A parallelogram has 2 parallel sides—those are the bases (b). The height (h) is the distance from one base to the other. Multiply those 2 values together and you've got the area of a parallelogram. For example, say you have a parallelogram with a base length of 4 m {\displaystyle 4m} {\displaystyle 4m} and a height of 2 m {\displaystyle 2m} 2m. Plug your numbers into the equation A = b h {\displaystyle A=bh} {\displaystyle A=bh} to get A = 4 ∗ 2 {\displaystyle A=4*2} {\displaystyle A=4*2}, then simplify to find an area of 8 m 2 {\displaystyle 8m^{2}} {\displaystyle 8m^{2}}. Remember: the height isn't the same as the length of the side! It's the straight-line distance between the top and bottom bases.

Trapezoid

Use A = b 1 + b 2 2 ∗ h {\displaystyle A={\frac {b_{1}+b_{2}}{2}}*h} {\displaystyle A={\frac {b_{1}+b_{2}}{2}}*h} to calculate a trapezoid's area. Since the 2 bases (b) of a trapezoid aren't the same length, the average is used for the area of this shape. Once you have the average length of the two bases, multiply that by the height (h)—the distance between the two bases—to easily find the area of a trapezoid. For example, say you've got a trapezoid with a bottom side of 5 m {\displaystyle 5m} {\displaystyle 5m}, a top side of 3 m {\displaystyle 3m} {\displaystyle 3m}, and a height of 6 {\displaystyle 6} 6. Start by adding the length of the two bases: 5 + 3 = 8 {\displaystyle 5+3=8} {\displaystyle 5+3=8}. Then, divide by 2 {\displaystyle 2} {\displaystyle 2} to get the average length of the bases: 4 {\displaystyle 4} 4. You've taken care of the first part of the formula! Now all you have to do is multiply the average length of the bases, 4 {\displaystyle 4} 4, by the height, 6 {\displaystyle 6} 6: 4 ∗ 6 = 24 {\displaystyle 4*6=24} {\displaystyle 4*6=24}. The area of your trapezoid is 24 m 2 {\displaystyle 24m^{2}} {\displaystyle 24m^{2}}.

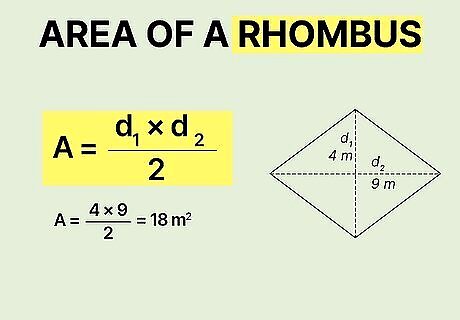
Rhombus

Get the area of a rhombus with A = ( d 1 ∗ d 2 ) 2 {\displaystyle A={\frac {(d_{1}*d_{2})}{2}}} {\displaystyle A={\frac {(d_{1}*d_{2})}{2}}}. In this formula, d 1 {\displaystyle d_{1}} {\displaystyle d_{1}} and d 2 {\displaystyle d_{2}} {\displaystyle d_{2}} refer to the length of 2 diagonal lines that you'll draw inside the shape between the opposite corners. Get the length of each of those 2 diagonals, multiply them together, then divide by 2. You've got the area of a rhombus! For example, say you have a rhombus with diagonals of 9 m {\displaystyle 9m} {\displaystyle 9m} and 4 m {\displaystyle 4m} {\displaystyle 4m}. You know that 9 x 4 = 36 {\displaystyle 9x4=36} {\displaystyle 9x4=36}. Divide 36 {\displaystyle 36} 36 by 2 {\displaystyle 2} {\displaystyle 2}. The area of your rhombus is 18 m 2 {\displaystyle 18m^{2}} {\displaystyle 18m^{2}}. What if the product of the diagonals is an odd number? No problem, just express your answer as a decimal. For example, a rhombus with diagonals of 3 c m {\displaystyle 3cm} {\displaystyle 3cm} and 7 c m {\displaystyle 7cm} {\displaystyle 7cm} has an area of A = ( 3 ∗ 7 ) 2 = 21 2 = 10.5 c m 2 {\displaystyle A={\frac {(3*7)}{2}}={\frac {21}{2}}=10.5cm^{2}} {\displaystyle A={\frac {(3*7)}{2}}={\frac {21}{2}}=10.5cm^{2}}.

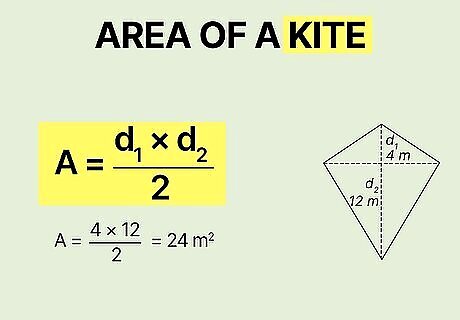
Kite

Find the area of a kite with A = ( d 1 ∗ d 2 ) 2 {\displaystyle A={\frac {(d_{1}*d_{2})}{2}}} {\displaystyle A={\frac {(d_{1}*d_{2})}{2}}}. A kite's orientation can throw you off because your "diagonal" lines (d1 and d2) might not look diagonal at all—they might actually be vertical and horizontal. But as long as they're connecting opposing corners, they're still called diagonals. Multiply them together and then divide by 2 {\displaystyle 2} {\displaystyle 2} to get your area. For example, say you have a kite with diagonals of 4 m {\displaystyle 4m} {\displaystyle 4m} and 12 m {\displaystyle 12m} {\displaystyle 12m}. Plug those values into the formula: A = ( 4 ∗ 12 ) 2 = 48 2 = 24 {\displaystyle A={\frac {(4*12)}{2}}={\frac {48}{2}}=24} {\displaystyle A={\frac {(4*12)}{2}}={\frac {48}{2}}=24}. The area of your kite is 24 m 2 {\displaystyle 24m^{2}} {\displaystyle 24m^{2}}.

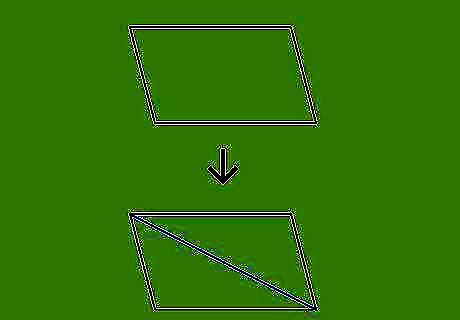
Any Quadrilateral Shape

Divide the quadrilateral into 2 triangles. If you draw a diagonal line from one corner to the other, you create 2 triangles within the quadrilateral. The 2 triangles might not be the same size, but they share a common base—the diagonal that divides the quadrilateral. If you're working on a homework problem, the diagonal line might already be drawn for you. In fact, if you have a quadrilateral with a diagonal line, that's a pretty big clue that you'll use triangles to find the area.

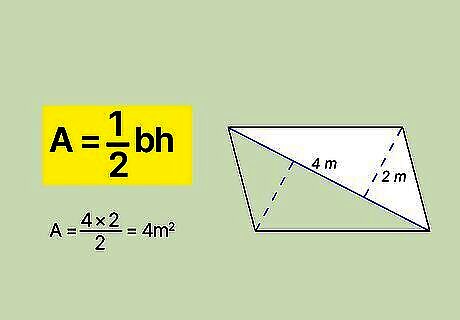
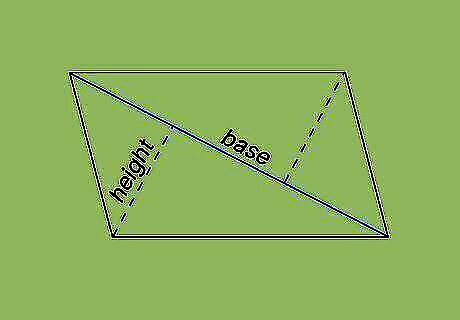
Get the measurements for the base and heights of your triangles. To find the area of a triangle, you need to know the size of the base (b) and the height (h). Your diagonal line is serving as the base of your triangles, so they'll both have the same measurement for the base. They might not be the same height, though, depending on the quadrilateral. The height isn't the length of a side (unless you're working with a right triangle). It's the length from the base to the top point of the triangle. If you're working a problem for homework and you're not given any way to measure these values, you can't use triangles to find the area of that quadrilateral.

Find the area of each triangle. Recall that the formula for the area of a triangle is A = 1 2 b h {\displaystyle A={\frac {1}{2}}bh} A={\frac {1}{2}}bh. All you have to do is plug in the measurements you got for the base and the height, then simplify the equation to find the area of each triangle. For example, say you have a diagonal with a length of 4 {\displaystyle 4} 4 that forms 2 triangles that each have a height of 2 {\displaystyle 2} {\displaystyle 2}. Your formula would be A = 1 2 ( 4 ) ( 2 ) {\displaystyle A={\frac {1}{2}}(4)(2)} {\displaystyle A={\frac {1}{2}}(4)(2)}, which simplifies to A = 1 2 ( 8 ) {\displaystyle A={\frac {1}{2}}(8)} {\displaystyle A={\frac {1}{2}}(8)}. So your answer would be A = 4 {\displaystyle A=4} {\displaystyle A=4}. In this example, both triangles have the same area since they both have the same base and height.

Add the areas of the 2 triangles together to get the area of the quadrilateral. Since you originally divided your quadrilateral into 2 triangles, all you have to do is add those 2 areas together and you'll have the total area of the quadrilateral. You could also think of the area of one of the triangles as being half the area of the quadrilateral. To return to the previous example, since each triangle has an area of 4 {\displaystyle 4} 4, you would simply add 4 + 4 {\displaystyle 4+4} {\displaystyle 4+4} to get 8 {\displaystyle 8} 8. Area is always expressed in square units. If the measurements in your original problem were meters, your answer would be 8 m 2 {\displaystyle 8m^{2}} {\displaystyle 8m^{2}}.