
views
X
Research source
Sound confusing? Don't worry, you can easily convert degrees to radians, or from radians to degrees, in just a few easy steps.
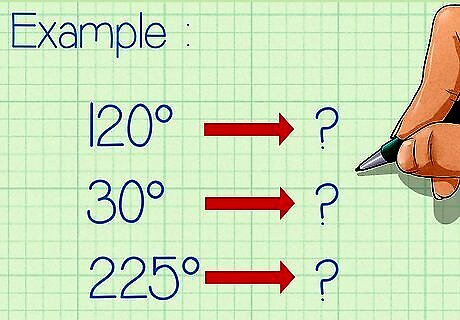
Write down the number of degrees you want to convert to radians. Let's work with a few examples so you really get the concept down. Here are the examples you'll be working with: Example 1: 120° Example 2: 30° Example 3: 225°
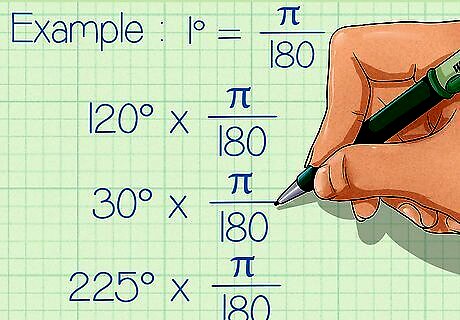
Multiply the number of degrees by π/180. To understand why you have to do this, you should know that 180 degrees constitute π radians. Therefore, 1 degree is equivalent to (π/180) radians. Since you know this, all you have to do is multiply the number of degrees you're working with by π/180 to convert it to radian terms. You can remove the degree sign since your answer will be in radians anyway. Here's how to set it up: Example 1: 120 x π/180 Example 2: 30 x π/180 Example 3: 225 x π/180
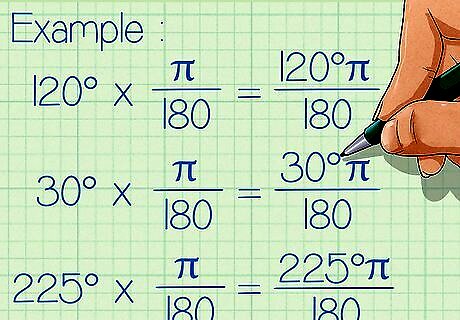
Do the math. Simply carry out the multiplication process, by multiplying the number of degrees by π/180. Think of it like multiplying two fractions: the first fraction has the number of degrees in the numerator and "1" in the denominator, and the second fraction has π in the numerator and 180 in the denominator. Here's how you do the math: Example 1: 120 x π/180 = 120π/180 Example 2: 30 x π/180 = 30π/180 Example 3: 225 x π/180 = 225π/180
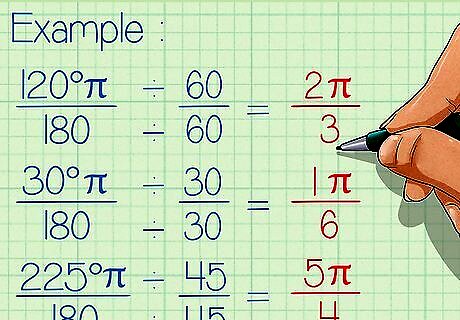
Simplify. Now, you've got to put each fraction in lowest terms to get your final answer. Find the largest number that can evenly divide into the numerator and denominator of each fraction and use it to simplify each fraction. The largest number for the first example is 60; for the second, it's 30, and for the third, it's 45. But you don't have to know that right away; you can just experiment by first trying to divide the numerator and denominator by 5, 2, 3, or whatever works. Here's how you do it: Example 1: 120 x π/180 = 120π/180 ÷ 60/60 = 2/3π radians Example 2: 30 x π/180 = 30π/180 ÷ 30/30 = π/6 radians Example 3: 225 x π/180 = 225π/180 ÷ 45/45 = 5/4π radians
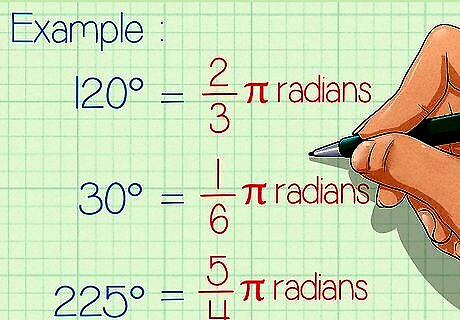
Write down your answer. To be clear, you can write down what your original angle measure became when converted to radians. Then, you're all done! Here's what you do: Example 1: 120° = 2/3π radians Example 2: 30° = 1/6π radians Example 3: 225° = 5/4π radians


















Comments
0 comment