
views

Identify the first, second, and last terms of the sequence. Typically, to solve a problem like this, you’ll be given the first 3 or more terms as well as the last term. For example, you may have the following sequence: 107, 101, 95…-61. In this case, the first term is 107, the second term is 101, and the last term is -61. You need all of this information to solve the problem.
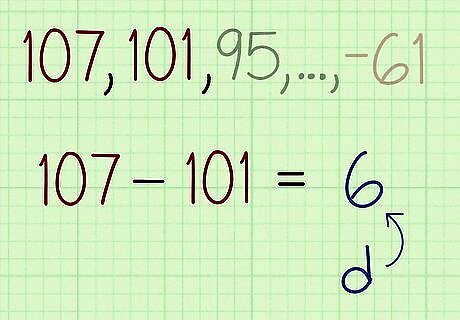
Subtract the first term from the second term to find the common difference. In the example sequence, the first term is 107 and the second term is 101. So, subtract 107 from 101, which is -6. Therefore, the common difference is -6.
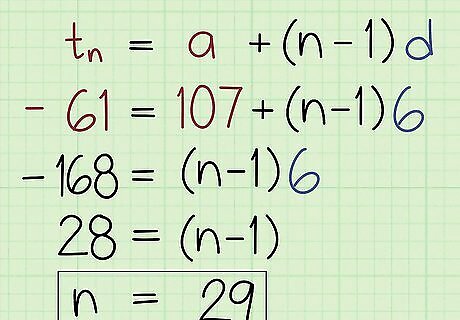
Use the formula tn = a + (n - 1) d to solve for n. Plug in the last term (tn), the first term (a), and the common difference (d). Work through the equation until you’ve solved for n. For example, start by writing: -61 = 107 + (n - 1) -6. Subtract 107 from both sides so you’re left with -168 = (n - 1) -6. Then, divide both sides by -6 to get 28 = n - 1. Finish by adding 1 to both sides so that n = 29.

















Comments
0 comment